| France hors IdF | ||||||
|---|---|---|---|---|---|---|
| km par personne par an | ||||||
| par actif | par adulte | |||||
| travail | travail | etudes | courses | autres | total | |
| km | ||||||
| très dense | 6 011 |
2 908 |
976 |
1 186 |
2 211 |
7 309 |
| densité intermédiaire | 7 854 |
3 602 |
1 106 |
1 506 |
3 194 |
9 436 |
| peu dense | 10 826 |
5 496 |
1 646 |
2 107 |
3 747 |
13 016 |
| très peu dense | 10 163 |
5 471 |
1 753 |
2 325 |
4 186 |
13 793 |
| total | 8 598 |
4 188 |
1 297 |
1 678 |
3 170 |
10 341 |
| relatif | ||||||
| très dense | 1 |
1 |
1 |
1 |
1 |
1 |
| densité intermédiaire | 1.3 |
1.2 |
1.1 |
1.3 |
1.4 |
1.3 |
| peu dense | 1.8 |
1.9 |
1.7 |
1.8 |
1.7 |
1.8 |
| très peu dense | 1.7 |
1.9 |
1.8 |
2 |
1.9 |
1.9 |
| total | 1.4 |
1.4 |
1.3 |
1.4 |
1.4 |
1.4 |
| Source : EMP 2019, 38.7M adultes (AGE>=18) dans la zone 10.1k observations dans EMP19 512 répétitions de rééchantillonage entre crochets : intervalle de confiance à 95% |
||||||
La Ville Compacte, une solution aux émissions de gaz à effet de serre
15007 mots.
1 L’impératif d’un habitat sobre
Réduire les émissions de gaz à effet de serre est aujourd’hui un objectif central des politiques publiques. Or, un tel objectif ne peut être atteint sans agir à différents niveaux et dans de nombreux domaines. Notamment, il ne va pas suffire de remplacer, au sein de notre système de production d’énergie, les sources fossiles par des sources renouvelables. Il faut aussi développer une stratégie de sobriété énergétique, de manière à réduire le coût de la bascule vers des énergies propres, à limiter l’empreinte environnementale liée à ces investissements dans le système énergétique actuel et, également, à éviter de produire de manière indirecte des émissions de gaz à effet de serre.
L’un des principaux enjeux autour de la sobriété est lié à l’habitat et à la mobilité des individus : quels modèles urbains promouvoir pour éviter ou limiter les déplacements énergivores ? Le Groupe Intergouvernemental des Experts du Climat (Lwasa, S. et al., 2022 ; Seto et al., 2014) a ainsi réaffirmé que la ville compacte est un des grands leviers de la transition vers des sociétés neutres en carbone. Cette position s’inscrit dans un long débat aussi bien aux Etats-Unis, où les défenseurs de la ville compacte s’opposent à l’étalement urbain (Ewing (1997) vs Gordon et Richardson (1997); Newman et Kenworthy (1989a)), qu’en Europe (Jenks, Williams et Burton, 1996) ou en Chine (Pan, Shen et Zhang, 2009) pour ne citer que quelques exemples emblématiques.
L’endroit où vivent les individus conditionne leurs émissions de gaz à effet de serre par deux canaux principaux : d’une part, les émissions liées au logement, au moment de sa construction puis celles induites par ses dépenses énergétiques, principalement le chauffage. D’autre part, la mobilité quotidienne pour accéder à l’emploi, à l’éducation et à toutes les aménités dont les ménages ont l’usage. On pourrait ajouter des liens plus difficiles à mettre en évidence entre le lieu de résidence et les comportements de consommation. Ainsi, l’effet « barbecue » ou « hypothèse de compensation » (Holden et Norland, 2005 ; Massot et Orfeuil, 2007 ; Muñiz, Calatayud et Dobaño, 2013 ; Orfeuil et Soleyret, 2002) voudrait que les ménages urbains se déplacent moins la semaine mais ont un besoin de nature ou un besoin de fuir la ville qui les conduit à faire plus de déplacements de loisirs les week-ends ou pendant les vacances. Une fois contrôlé des plus importantes variables socio-économiques, un ménage urbain prend effectivement plus souvent l’avion pour les vacances et, plus marginalement, effectue des déplacements plus longs le week-end qu’un ménage vivant à la campagne. Toutefois, les citadins n’effectuent pas ces déplacements pour satisfaire un besoin de nature ou pour fuir la ville, puisque les destinations sont souvent d’autres villes (Munafò, 2017). La mobilité occasionnelle des citadins doit plus s’interpréter comme la traduction de leurs goûts pour les expériences diverses, contrastées et cosmopolitiques, qui expliquent leur désir de vivre dans des centres urbains. Il reste que la hausse des kilomètres attribuables à cet effet « barbecue » est marginal (un facteur 10) en regard de la différence de kilomètres parcourus entre un ménage urbain et un ménage rural. Il faudrait également tenir compte du cas d’un ménage s’éloignant de l’emploi mais qui compense en télétravaillant. Pour l’heure, il est encore difficile de dresser un réel bilan kilométrique de ces cas (Cervero, 1989 ; Orfeuil et Soleyret, 2002).
Les postes « mobilité » et « logement » couvrent plus de 50% de l’empreinte carbone des ménages. Selon le SDES (Baude, 2022), la mobilité représentait 30% de l’empreinte carbone d’un français en 2017. L’empreinte carbone inclue les émissions directes et indirectes et s’élevait en 2017 à 9,5 tCO2eq/an par habitant en France. Les émissions liées au logement représentent 23% de l’empreinte totale. L’empreinte carbone de la mobilité se décompose en 60% (18% de l’empreinte totale) d’émissions directes par la combustion de fossiles, 19% (5,7% de l’empreinte) pour la construction et l’entretien des véhicules. Le transport aérien compte pour 10% (6% de l’empreinte). La part restante (11% et 6,6% de l’empreinte) est liée aux services de transport directs ou indirects que les ménages consomment (Baude, 2022, p. 16).
L’enjeu est donc clair et les leviers sont nombreux (Hsu et al., 2023). Pour les consommations résidentielles : une plus grande efficacité thermique des bâtiments, des températures cibles plus basses l’hiver, un moindre recours à la climatisation l’été et une moindre utilisation de l’eau chaude. Pour la construction des bâtiments : la décarbonation de la construction, des normes d’efficacité énergétique pour les nouveaux bâtiments, une limitation des constructions nouvelles, l’utilisation du bâti existant ou le partage du bâti existant en réduisant l’espace alloué par personne ou en multipliant les usages d’un local au cours d’un cycle. Pour les mobilités : l’électrification des véhicules, la hausse de l’occupation moyenne des véhicules (covoiturage, transport en commun), le passage à des mobilités douces (vélo ou marche) et, enfin, la réduction des distances parcourues, soit par la baisse de la fréquence des trajets, soit par le raccourcissement des trajets en habitant plus près des emplois et services.
Le modèle de la ville compacte (Jenks, Williams et Burton, 2003) paraît répondre à chacun de ces enjeux en combinant l’utilisation de nombreux leviers. En regroupant activités et résidents, la forme urbaine réduit a priori les distances, fournit les services et les activités dans un voisinage accessible sans voiture, permet des transports en commun rentables et denses et réduit de nombreux coûts (entretien des routes et des réseaux en tout genre, services de livraison, gestion des déchets, etc.). Toutefois, ce modèle urbain a ses adversaires, qui interprètent celle-ci sous des formes repoussantes (tours gigantesques, espace privé minuscule, etc.) comme si la compacité ne pouvait se matérialiser que d’une unique façon. Depuis l’invention du terme (attribué à Dantzig, Dantzig et Saaty, 1973), la controverse entre un modèle de ville fondé sur l’usage de la voiture, dans lequel les gains de vitesse apporté par la technologie invitent à l’étalement, et un modèle organisé pour exclure la voiture des mobilités quotidiennes est vive.
Cette controverse a, au cours des 50 dernières années, pris plusieurs formes. La notion de ville fonctionnelle (dans la lignée de Janes Jacob (Jacobs, 1961) et contre Le Corbusier) a trouvé dans le New Urbanism un argument fondé sur les préférences des individus et le développement organique des villes, poussé par les besoins des habitants. L’étalement urbain serait alors une manifestation d’un désir d’être entre-soi de certains groupes sociaux : ainsi des riches évitant les pauvres et des blancs fuyant les noirs (Levine, 2010). La question climatique, par l’injonction à la sobriété, est un autre terrain d’affrontement entre ces deux visions radicales de la ville. Cet affrontement prend une nouvelle dimension en opposant non plus seulement étalement urbain et ville compacte, mais aussi ville compacte et mode de vie sobre avec une faible division du travail et une grande autonomie – parfois appelé décroissance ou post-croissance urbaine (Savini, Ferreira et von Schönfeld, 2022).
Outre la question climatique, l’usage la voiture, notamment thermique, au sein des villes apporte son lot de problèmes : pollution de l’air, congestion, accidents de la route, qui tous impactent négativement la santé humaine. Dans un contexte de hausse des coûts relatifs de l’énergie à court et à long terme, les mobilité quotidiennes et la consommation d’énergie résidentielle exercent une contrainte de plus en plus importantes sur les budgets des ménages. La répartition spatiale étant conditionnée notamment par les prix de l’immobilier, les choix de localisation peuvent être fait sans pouvoir anticiper correctement les évolutions des coûts futurs et induire un enfermement de certaines populations, souvent modestes, dans des zones excentrées qui finiront par entraîner des coûts de transport difficilement soutenables. La facilité d’accès à l’emploi et à d’autres aménités en fonction de son lieu de résidence –- que l’on peut mesurer par l’accessibilité –- détermine les pratiques de mobilités des résidents : les modes de transport possibles, les coûts de chaque trajets, l’activité physique induite, ou encore la possibilité pour des individus ne pouvant pas conduire (comme les plus jeunes) d’accéder aux aménités de manière autonome.
L’argument environnemental pour les villes compactes repose sur une empreinte carbone plus faible pour des déplacements plus courts et plus doux que dans le cas de l’étalement urbain ou dans le cas d’une mégalopole où les distances s’allongent malgré une densité importante. Dans ce débat, une littérature assez récente (depuis les années 2000) a versé un grand nombre d’arguments empiriques en utilisant les données de grandes enquêtes auprès des ménages sur les mobilités. Il en ressort un diagnostic mitigé : une plus grande densité est bien associée à de moindres déplacements, mais cette conclusion est fragile en raisons de nombreuses difficultés méthodologiques (liées à l’endogénéité des variables et à des biais de sélection). Plus encore, l’effet identifié semble faible – une élasticité de -0,1 entre densité et nombre de kilomètres parcourus – au point qu’il est illusoire de compter sur la hausse de la densité pour réduire les émissions Duranton et Turner (2018).
Nous présentons dans la section suivante cette littérature, les principaux résultats ainsi qu’une analyse critique des méthodes qui conduisent au résultat principal. Nous présenterons ensuite une approche alternative, s’attachant à mieux définir la notion de densité et surtout à préciser ce qu’augmenter la densité veut dire, pour montrer qu’il s’agit bien d’une levier efficace pour réduire les émissions liées à la mobilité, conformément à l’intuition initiale de Newman et Kenworthy.
2 Une densité plus élevée fait-elle baisser les émissions ?
Le lien entre la géographie, la forme urbaine et les mobilités résidentielles a donné lieu à un débat nourri, vieux de quelques décennies et persistant. Tout le monde a en tête les travaux et le graphique de Newman et Kenworthy (figure 1) (Newman et Kenworthy, 1989a, 1989b, 1999) représentant une corrélation négative entre consommation d’énergie annuelle de carburant et densité, qui a confortée l’intuition que les villes compactes sont plus soutenables que les villes « étalées ». Le graphique de (Newman et Kenworthy, 1999) a été largement critiqué et la corrélation affichée sur le graphique a été jugée en partie fallacieuse du fait de nombreux facteurs, dont le niveau de développement de chacune des villes considérées, le prix local du carburant ou d’autres facteurs explicatifs communs (Ewing et al., 2017). En 2015, Ewing et Hamidi (2015) recensaient plus de 200 études empiriques et 12 revues de littérature sur ce sujet. Plusieurs éléments à la fois théoriques, méthodologiques et empiriques ont été raffinés et conduisent à un résultat pour le moins mitigé selon lequel l’influence de la densité ou d’autres dimensions de la forme urbaine sur les consommations de carburant seraient trop petits pour jouer un rôle prépondérant dans la réduction des émissions de gaz à effet de serre.
Ainsi, l’affirmation initiale s’est trouvé « anesthésiée » et il faudrait croire que le lien entre densité et empreinte carbone est trop faible pour justifier une politique urbaine. Une telle anesthésie a été possible parce que la densité est plutôt un mauvais indicateur de la forme urbaine ; c’est un indicateur équivoque. Les critiques méthodologiques de l’article de Newman et Kentworthy sont certes justifiées, mais leur intuition exige un examen qui ne se limite pas à redéfinir la mesure de la densité urbaine. Par exemple, des quantification centrées sur l’accessibilité à l’emploi ont un meilleur pouvoir explicatif. Mais, plus encore, il faudrait surtout démêler deux questions : celle de savoir si toute densification, en général, entraîne nécessairement une réduction des émissions – la question qui a monopolisé l’attention – et celle de savoir quels scénarios de densification apportent un niveau de réduction suffisant pour justifier une politique publique.
2.1 Quantifier la forme urbaine
La densité de population, l’indicateur retenu par Newman et Kenworthy (1989a), ne suffit pas à décrire la forme et la structure des villes. La même distribution spatiale de la densité peut cacher des formes urbaines très diverses. Depuis Cervero et Kockelman (1997), les indicateurs complémentaires à la densité ont été catalogué et sont généralement appelés les D. Aux 3 D initialement proposés par Cervero et Kockelman, pour Densité, Diversité et Design, ont été ajouté d’autres D comme la distance au centre des emplois (Central Business District) ou la distance aux transports en commun (le plus proche, un indicateur de connectivité, etc…). Une plus grande densité devrait induire moins de kilomètres parcourus par résident, du moins si l’on mesure la densité à la bonne échelle, de manière à rendre compte de la proximité des centres d’intérêt des résidents.
Le terme « densité » recouvre ainsi différentes notions : la densité peut être celle des habitants, des logements, des bâtiments ou de la surface habitable. Elle peut être calculée à différentes échelles et éventuellement lissée, conduisant à des résultats sensiblement différents puisque les tissus urbain sont toujours très hétérogènes sur un territoire donné. La façon la plus immédiate de calculer la densité est de prendre le ratio entre le nombre d’habitants et la surface bâtie, pour une zone donnée, mais il est également possible de calculer la densité moyenne en pondérant la densité sur une maille (régulière ou non) par le nombre d’habitants résidents dans cette maille. Cette densité pondérée par la population (PWD), parfois appelée « densité articulée », rend mieux compte de la densité moyenne ressentie par les résidents. Par exemple, la densité moyenne simple de New York dans son ensemble est plus faible que celle de Los Angeles alors que la densité pondérée par la population met New York au dessus de Los Angeles en termes de densité, puisque les résidents de Manhattan sont nombreux a percevoir que la densité de Manhattan est forte.
Le deuxième D –- la diversité –- cherche à tenir compte de la spécialisation de l’environnement urbain. Dans beaucoup de villes américaines, du fait d’une politique persistante de zonage peu pratiquée en Europe (Hirt, 2012), les espaces sont spécialisés, en particulier entre zones de résidences et de commerce ou d’activité économique. La diversité, mesurée par exemple par (l’opposé d’) un indice de Herfindahl, permet de rendre compte de l’imbrication des services ou des opportunités d’emplois avec les lieux de résidence. Là encore, l’échelle de prise en compte de la diversité est un point important et, à nouveau, l’imbrication peut être pondérée pour mieux rendre compte des perceptions. Tout comme pour la densité, on s’attendrait à ce qu’une plus grande diversité soit associée à moins de kilomètres parcourus.
Le troisième D –- le design –- fait référence à la configuration des rues, des routes ou du réseau de transport. Une configuration de routes peu denses, composé d’axes traversant continus et à fort débit est peu propice à la marche. Un réseau de ruelles entourant des blocs de bâtiments plus petits permet au contraire une circulation capillaire. La mesure du design passe par des indicateurs variés comme le nombre d’intersection, la taille des blocs. Alternativement, (Blaudin de Thé, Carantino et Lafourcade, 2021) utilisent la dimension fractale des bâtiments1.
1 La dimension fractale est définie comme la pente du ratio entre le nombre de bâtiments et le nombre de pavés lorsque la taille du pavage varie et tend vers 0 (éventuellement en log).
La distance au centre des emplois (CBD) est une mesure assez simple dès lors qu’on peut identifier facilement le centre de l’emploi. Malheureusement, le modèle monocentrique qui justifierait cette mesure décrit très mal la plupart des villes et elle est très insatisfaisante dans le cas général. Malgré cela, le nombre de kilomètres voyageurs (VKT) est corrélé fortement à ce type de mesure (voir plus bas).
La distance aux transports en commun est également simple conceptuellement. On retient généralement la distance au plus proche arrêt de transport en commun ou le nombre d’arrêt dans un périmètre donné (par exemple 10 minutes de marche). C’est toutefois un indicateur assez frustre puisqu’il ne suffit pas de résider près d’une station de métro ou d’un arrêt de bus, il faut encore que le transport desserve les bonnes destinations aux bons moments. Ceci dit, cette mesure est renseignée dans les enquêtes de mobilité (comme l’Enquête Mobilité Certifiée CEREMA, EMC2) et elle peut être intéressante une fois associée aux données sur les réseaux de transports (de type GTFS).
En décrivant la forme urbaine par ces grandeurs, on dispose d’indicateurs qui sont principalement locaux et associés à l’endroit de résidence. Ils peuvent être calculés à différentes échelles, comme dans l’analyse multiniveaux de Lee et Lee (2020), mais aucun de ces indicateurs n’éclaire réellement la capacité systémique des infrastructures d’une ville à relier les résidents à leurs lieux d’intérêt, emplois ou aménités.
2.2 Endogénéité et autosélection des résidents
Bien qu’il soit délicat de tirer une conclusion simple et univoque du large panel d’analyses sur le lien entre densité et émissions, des mesures de la forme urbaine comme la densité d’habitants ou d’emploi, parfois des mesures plus complexes comme la dimension fractale du bâti (Blaudin de Thé, Carantino et Lafourcade, 2021), la diversité locale de l’emploi, des indicateurs de centralité, de connectivité ou de continuité (Ewing et Hamidi, 2015) sont corrélées négativement avec le nombre de kilomètres-voyageurs (abrégé en VKT pour Vehicule Kilometers Traveled ou Vehicule Miles Traveled dans la littérature en langue anglaise).
L’évaluation du lien causal demeure délicate en raison de possibles biais de sélection des résidents : dans quelle mesure les ménages qui de moindres revenus et se trouvent contraints à des déplacements plus courts et non motorisés habitent-ils des zones plus denses et des logements plus petits et plus proches du centre-ville ? Ou encore, les individus effectuent-ils de longs trajets en voiture parce qu’ils habitent loin ou, à l’inverse, est-ce qu’ils résident loin parce qu’ils aiment faire de la voiture ? Autant de questions qui fragilisent l’établissement d’un lien causal entre densité et VKT. En général, dans ces études, la corrélation est considérée en partie comme causale mais faible. (Duranton et Turner, 2018) concluent ainsi pour les Etats-Unis à une élasticité de l’ordre de -0.1 entre densité et kilomètres parcourus. (Holian, 2020) dans la suite de (Grazi, Bergh et Ommeren, 2008) utilise une variable instrumentale astucieuse (le fait d’avoir des enfants de même sexe permet de les loger dans une même chambre et offre à ces ménages plus de choix résidentiel sans lien avec leurs préférences de déplacement) et concluent à une élasticité proche de celles rapportées dans la littérature, à ceci près qu’ils mesurent un effet local moyen sans pouvoir séparer des contextes urbains très différents. On retiendra toutefois que le biais d’endogénéité qu’ils identifient reste assez faible.
Le tableau suivant (tableau 1) est extrait de la méta-analyse de (Stevens, 2017) qui synthétise la littérature en essayant de prendre en compte la diversité des mesures possibles pour calculer des élasticités comparables. L’autosélection des individus, c’est-à-dire le fait que les ménages sont triés spatialement en fonction de leurs préférences et de leurs revenus, se traduit par une élasticité des kilomètres-voyageurs à la distance au centre-ville ou à la densité plutôt supérieure lorsqu’elle est prise en compte. L’élasticité à la densité de population est plutôt faible bien que supérieure à celle de Duranton et Turner (2018).
Au vu des résultats reportés dans ce tableau, il est peu vraisemblable que la hausse de la densité puisse réduire significativement les émissions de gaz à effet de serre, puisque son élasticité est au mieux de -0.22 et qu’il faudrait une multiplication par 2.5 de la densité de population pour réduire les kilomètres-voyageurs de 50%.
| Variable mesurée (D) | Elasticité des km-voyageurs (VKT) à D avec/sans autosélection |
N études avec/sans autosélection |
|---|---|---|
| Distance au centre-ville (CBD, downtown, centre géographique, barycentre de l’emploi, des habitants) | -0.63/-0.34 | 3/14 |
| Densité de population ou de ménages | -0.22/-0.10 | 5/19 |
| Accessibilité à l’emploi en voiture | -0.20 | 0/10 |
| Densité des intersections ou des rues | -0.14 | 1/15 |
| Mélange des usages (diversité) | 0.11/-0.033 | 2/15 |
| Densité des emplois | -0.07/-0.01 | 2/11 |
| % d’intersections entre 4 voies | -0.06 | 1/4 |
| Distance à l’arrêt de transport en commun le plus proche | -0.05 | 5AR/12 |
| Accessibilité aux emplois par les transports en commun | 0.00 (ns) | 0/3 |
| Déséquilibre entre les emplois et les résidents | 0.00 (ns) | 0/8 |
Une première conclusion tirée des analyses empiriques est donc qu’il existe un effet des variables quantifiant la forme urbaine et que le signe de cet effet est généralement tel qu’attendu. Une forme urbaine plus compacte induit moins de kilomètres-voyageurs parcourus. La prise en compte de l’autosélection et l’utilisation de variables instrumentales peuvent modifier les estimations des élasticités, mais les modifications sont petites et n’invalident pas la première conclusion.
La seconde conclusion importante est que plusieurs facteurs jouent et qu’il faut probablement les combiner pour arriver à une réduction significative des émissions de gaz à effet de serre. Cette conclusion est sans doute un peu décevante et intègre le fait que l’étalement urbain n’est pas inéluctablement un facteur d’augmentation des émissions. Les études empiriques ne parviennent pas à un résultat tranché parce que la diversité des situations observées est grande. Sur le plan théorique on peut également imaginer que des effets d’équilibre général jouent un rôle important. Les individus peuvent vivre dans des zones peu denses mais avoir un accès à des centres d’emplois à des distances raisonnables. Les concentrer dans des pôles urbains peut accroître les mouvements pendulaires. (Gaigné, Riou et Thisse, 2012) développent un modèle avec plusieurs centre d’emploi et montrent que la concentration n’a pas toujours l’effet attendu de réduire les kilomètres si on n’assigne pas les individus à aller au plus proche. Par ailleurs, la bi-activité des ménages peut rendre impossible l’optimisation des distances à moins de proposer une très forte concentration des résidences et des emplois au même endroit.
La troisième conclusion que l’on peut tirer de ces analyses est que la quantification de l’étalement urbain ou de son opposé, la compacité urbaine, est un exercice difficile et qui n’a pas été conduit à son terme. Il s’agit de relier d’une part la distribution spatiale des habitants, de l’autre celle des emplois et des différents services comme les écoles ou les commerces de proximité, de prendre en compte les possibilités de transport offertes en chaque point du territoire tout en intégrant d’autres contraintes comme la congestion des transports, les conséquences pour la santé, les îlots de chaleurs, et ainsi de suite. Or cette complexité ne peut pas se résumer à quelques indicateurs agrégés ou strictement localisés. Et, pour les mêmes raisons, les politiques publiques ne peuvent pas se concevoir ou s’évaluer uniquement à travers un prisme qui écraserait toute l’information nécessaire pour retranscrire la réalité d’une géographie urbaine donnée.
Comme le notent de nombreux auteurs Stevens (2017), la distance au centre des emplois (CBD) joue un rôle plus important que d’autres facteurs2. Toutefois, cette notion est d’un intérêt limité Elle est pertinente pour les formes urbaines monocentriques ou encore lorsque la concentration spatiale de l’emploi est importante, mais elle devient trompeuse lorsque les formes urbaines sont plus complexes et, plus encore, pour des zones urbaines de grande taille. Prenons le cas de l’agglomération parisienne, où pourtant l’hypercentre joue un rôle éminent. On ne peut pas considérer que l’emploi est particulièrement concentré sur l’Île de la Cité ou l’Île Saint Louis. L’emploi est diffus sur une large zone, avec des zones plus concentrées comme la rive droite (Opéra, Havre-Caumartin, Champ-Elysées), la Défense ou encore Saint-Denis. Plus encore, cette concentration est toute relative et il y a de l’emploi un peu partout, que ce soit des emplois liés à la présence de résidents ou liés à des équipements non centraux (un hôpital, une université, un pôle administratif privé ou public, une zone commerciale, etc…).
2 Il est délicat de comparer les élasticités de variables aussi disparates que la densité et la distance au centre. Dans le cas d’une densité uniforme de population sur une cercle de rayon r, la densité (N/{\pi r^2}) et la distance moyenne au centre du cercle (\pi r^2) sont inversement proportionnelles. Dans ce cas, il est simple de passer d’une élasticité à l’autre et, donc, de les comparer. Mais si l’on prend une densité gaussienne, le ratio entre la densité et la distance moyenne pondérée par la population est proportionnel au paramètre de dispersion de la densité (\sigma). Il est alors facile de construire, avec des distributions plus ou moins concentrées, pour une même densité, une grande palette de distances moyennes. La comparaison des élasticités n’est plus lisible et dépend d’un autre paramètre.
D’après FLORES (INSEE), en 2021, les 9 arrondissements à 1 chiffre concentrent un peu plus de 800 000 emplois salariés sur les 4,26 millions que compte la région Ile-de-France. L’emploi salarié dans les arrondissements centraux représente 19% de l’emploi de la région pour moins d’1% de la surface. Il y a indéniablement concentration spatiale. Pour autant, plus de 80% des emplois salariés sont à l’extérieur de ce petit noyau central. Ce qui est vrai pour Paris l’est pour toute grande agglomération, de Tokyo à Los Angeles, et fait du modèle monocentrique une approximation grossière, qui n’est pertinente que pour quelques agglomérations de petite taille et de structure spécifique.
Ne pas pouvoir prendre en compte la répartition spatiale de l’emploi et des activités dans toutes les dimensions est également un frein à une analyse des politiques publiques dont l’objet est souvent le développement de telle ou telle zone, pour des raisons diverses allant de la stratégie d’aménagement générale de la zone urbaine, de son articulation avec les réseaux de transport, à la réhabilitation de terrains, selon leur disponibilité ou leur prix. La décision publique ne se limite pas à plus de densité en général et il faut que l’analyse s’appuie sur ce qui compte localement.
3 Pourquoi et comment projeter ?
3.1 Pourquoi ?
C’est à partir de la troisième conclusion (la difficulté de la quantification) que nous proposons une approche différente du lien entre densité et kilomètres parcourus. Au lieu de partir d’observations individuelles ou agrégées de mobilité, qui associent des déplacements à des informations sur la forme urbaine générale ou locale pour quantifier avec plus ou moins de bonheur un lien causal, nous proposons d’expliciter par une modélisation l’articulation entre les distributions spatiales des habitants, des emplois et des aménités, en tenant compte de la géographie et des infrastructures de transport.
La méthode s’apparente à celles recensées par (Rodier, 2009) dans lequel on utilise un modèle dit de « Land Use Transport Interaction » (LUTI) pour analyser sur une zone urbanisée les effets de modification de la forme urbaine, de changement dans les infrastructures, de changement de comportement ou de politiques diverses, comme la taxation de l’essence ou le péage urbain. Idéalement la modélisation est robuste c’est-à-dire que les différentes briques qui la composent sont soumis à une analyse de causalité et on suppose que le biais de modélisation (phénomènes omis, granularité temporelle ou spatiale de de la représentation) n’est pas trop fort.
Cette démarche est celle des sciences du climat et Masson et al. (2014) en discutent la validité pour l’analyse des villes et du changement climatique. Plus généralement, dès que l’on a affaire à des systèmes complexes (Thurner, Klimek et Hanel, 2018), on est confronté à une double difficulté : d’un côté, les causalités s’imbriquent et toute analyse empirique devient difficile voire impossible à moins que l’on dispose de sources de variations aléatoires qui ramènent à un cas quasi-expérimental. Lorsque c’est le cas, les expériences quasi naturelles observables doivent être suffisamment nombreuses pour produire des conclusions généralisables. De l’autre côté, il n’est pas assuré qu’un système complexe puisse être décrit par des relations simples entre quantités macroscopiques. Il existe quelques exemples de telles propriétés émergentes, sous des conditions de validité bien définies, comme la fameuse loi de Boyle-Mariotte . Mais, dans le cas général, un système complexe est toujours plus riche que la description macroscopique. Ces deux arguments se recoupent partiellement, l’approche par quasi expérience étant d’autant plus généralisable que des lois macroscopiques valides et pleine de signification émergent du système complexe.
L’approche par modélisation, suivie de validation des briques par des (quasi-)expériences naturelles, des simulations numériques ou des analyses des propriétés, est alors une méthode pertinente poursuivie, entre autres, par (Batty, 2013 ; Bettencourt, 2021) ou encore dans les modèles LUTI. Le recours à des microfondations, décrivant plus en détail la complexité du système, n’est pas pour autant la garantie d’une meilleure compréhension, ni d’une représentation exempte de biais. La modélisation doit être parcimonieuse et ne pas se transformer en boîte noire. La simulation numérique rend difficile la compréhension de la modélisation surtout lorsque celle-ci se déploie dans des espaces numériques de grande dimension. De plus, la profondeur du modèle doit être fonction de la nature des données que l’on a à sa disposition. Un modèle qui repose sur une paramétrisation qui dépasse de loin la dimension des observations court le risque du surapprentissage, parce qu’il existe plus de paramètres à calibrer que d’observations indépendantes. Le surapprentissage peut donner le sentiment que l’on explique bien les observations, mais c’est au prix d’une impossibilité de généralisation, ce qui est précisément ce que l’on cherche à faire par la modélisation.
Les briques de la modélisation structurelle que nous allons mettre en place sont multiples et s’inspirent de la construction du modèle à 4 étapes (Hensher et Button, 2007 ; Patrick Bonnel, 2001). Les quatre étapes sont : la génération du nombre de trajets en partance de chaque origine (les résidences), et des trajets qui arrivent à chaque destination (les emplois, les aménités). La deuxième étape distribue ces trajets sur l’ensemble des paires origine-destination. La troisième étape est celle du choix modal de chacun des trajets et la quatrième vise à déterminer le tracé du trajet, compte tenu de l’origine, de la destination et du mode de transport. Comme nous le verrons, l’articulation de ces briques se ramène en fait à un simple emboîtement de probabilités conditionnelles, ce qui souligne à la fois que cette modélisation est finalement plus simple qu’il n’y paraît et que le modèle à 4 étapes a probablement été développé à partir de l’intuition que chacune des étapes n’est qu’une étape de calcul de la probabilité de trajets, qui est la colonne vertébrale de la modélisation.
Notre méthodologie, développée dans Parodi et Timbeau (2023), reprend cette approche. La première étape consiste à localiser les résidents (à partir des données carroyées de l’INSEE (INSEE, 2022a)), les emplois (à partir de INSEE (2022b) (MOBPRO) et des fichiers fonciers pour une imputation infra-communale). Nous calculons ensuite les distances et les temps de trajets pour les 4 modes considérés (marche, vélo, transport en commun, voiture, mais pas de trajets multimodaux hors ceux avec la marche à pied) – ce qui anticipe l’étape 4 – entre toutes les résidences (les origines) et tous les emplois (les destinations). Par analogie avec un modèle radiatif (Simini et al., 2012 ; Stouffer, 1940), MEAPS nous permet de répartir les flux de « navetteurs » et d’affecter à chaque résident une distribution de probabilité sur le lieu où il travaille sur la base des distances, du nombre de résidents et de la quantité d’emploi sur le territoire considéré. Ce modèle radiatif est augmenté d’un processus de saturation et de priorité (MEAPS) de façon à assurer de façon explicite et paramétrable que chaque résident occupe un emploi et un seul et que tous les emplois sont occupés. Nous avons montré dans Parodi et Timbeau (2023) que ce modèle permettait de mieux rendre compte des flux e navetteurs entre communes mesurés par MOBPRO que le modèle gravitaire par la prise en compte de la géographie des résidents, des emplois et des réseaux, du moins sur le territoire de La Rochelle.
Il n’en reste pas moins que si Parodi et Timbeau (2023) permet de reproduire MOBPRO et d’en proposer une interpolation à la maille du carreau INSPIRE à 200m, il faut utiliser plus d’informations pour déterminer la quantité globale de déplacements, c’est-à-dire le nombre de kilomètres parcourus annuellement par un résident moyen d’un carreau donné. L’approche par MEAPS ne donne en effet que le flux (ou une probabilité) de personnes d’une résidence vers un emploi, à une distance donnée, mais sans préciser la fréquence de ces déplacements. Cette information n’est pas dans MOBPRO et rend approximatif la détermination des kilomètres parcourus sur cette seule base. Nous proposons ici une approche qui résout cette indétermination en modélisant le nombre de trajets et en introduisant des caractéristiques socio-économique des individus, ce qui permet d’ajouter une couche supplémentaire à l’analyse spatiale par MEAPS.
Pour ce faire, il faut examiner les pratiques de mobilité des Français. Nous nous appuyons ici sur l’enquête mobilité des personnes SDES (2021) (EMP 2019). Cette enquête ne permet pas d’analyses locales, parce que l’échantillon est trop petit et le tirage aléatoire n’a pas été conçu pour un tel usage. Elle permet en revanche d’associer les caractéristiques des individus, de leur ménage, de leur équipement en véhicule aux trajets effectués pour différents motifs. Il est alors possible de modéliser leurs pratiques de mobilités selon ces caractéristiques. En associant la méthode MEAPS à cette analyse, on pourra alors évaluer au carreau les kilomètres parcourus par chaque résident et procéder à des agrégations à tous les niveaux souhaités en exploitant au maximum l’information contenue dans EMP 2019, dans MOBPRO, dans la localisation fine des résidents, selon leurs caractéristiques socio-économique et des emplois et dans la géographie des réseaux.
La modélisation retenue suppose que les réseaux, la position des habitants, des emplois ou des aménités est considérée comme exogène. Endogénéiser ces éléments, sous contrainte du respect des zonages et des règlements d’urbanisme, compliquerait exagérément la modélisation. Il faudrait introduire des dynamiques longues, celles de la localisation des habitants, de la construction de nouveaux logements, de la création de nouvelles zones d’activité, qui s’imbriquent avec d’autres plus courtes comme les flux résidence-emplois ou les modes de transport. Il est difficile – voire impossible – de calibrer les paramètres qui président aux dynamiques longues, pour lesquelles on dispose de trop peu d’éléments. Le développement urbain dépend de choix politiques qui ne peuvent être aisément anticipés. Cela conduit également à distinguer des horizons temporels variés dans lesquels on modélise des dynamiques transitoires multipliant les informations à représenter. En fixant ces éléments de dynamique longue, on simplifie la représentation en renvoyant l’analyse de ces dimensions à l’élaboration de scénarios exogènes qui ignorent les causalités entre par exemple une nouvelle ligne de transport et le développement des zones d’activité.
3.3 Retour sur l’autosélection et le biais d’endogénéité
Aupavant, il vaut revenir sur les problèmes méthodologiques des méthodes retenues habituellement dans la littérature (cf. section 2), dont nous avons rappelé les résultats plus haut dans le texte, pour mieux apprécier notre approche. La stratégie usuelle consiste à estimer pour chaque individu observé le lien entre, d’un côté, les kilomètres qu’il a parcourus et, de l’autre, ses caractéristiques socio-économiques ainsi que quelques indicateurs géographiques supposés adéquats pour rendre compte de la densité urbaine. Le problème de cette perspective est qu’elle s’abstrait d’emblée de la géographie réelle pour n’en retenir que quelques descripteurs comme la densité urbaine, le design, la diversité ou encore la distance au centre des affaires. Ce faisant, les données du problème sont comme « agrégées » selon les niveaux de densité et les niveaux de tous les autres descripteurs géographiques retenus ; au passage, la géographie réelle est « écrasée ». On peut se représenter la réduction qui est opérée de la manière suivante : les données géographiques peuvent être représentées par une carte remplie de données géolocalisées, voire deux cartes si l’on s’intéresse à des flux, avec des données sur les points de départ et d’arrivée. Cette carte est comme un grand tableau de données. Toutefois, ce n’est pas sur ce tableau que les estimations usuelles vont être effectuées ; c’est sur le tableau réduit où l’on a mis dans la même case les individus aux caractéristiques socio-économiques et aux niveaux de descripteurs géographiques identiques. Or, cette réduction n’est pas sans conséquence. Elle est au contraire l’une des sources des nombreux doutes méthodologiques qui « travaillent » la communauté des spécialistes du domaine. Les interrogations sur l’endogénéité remettent typiquement en question la similitude supposée des individus appartenant à une même case du tableau réduit.
Pour le comprendre, il faut revenir à la formulation classique du problème, où il s’agit d’estimer le nombre km_i de kilomètres parcourus (parfois en log) par un individu i en fonction des j caractéristiques socio-économiques X_i^j, des k descripteurs géographiques locaux L_{local(i)}^k et des l descripteurs globaux G_{global(i)}^l.
km_i = \alpha_j X_i^j + \beta_k L^k_{local(i)} + \gamma_l G^l_{global(i)} + \varepsilon_i \tag{4}
Un problème d’endogénéité survient lorsque la densité – une des composantes du vecteur L^k_{local(i)} ou du vecteur G^l_{global(j)} – est corrélée avec certaines caractéristiques socio-économiques X^j_i, ce qui induit un biais dans l’estimation du coefficient \beta_k. Pour savoir si l’on se heurte à un problème d’endogénéité, il faut donc se poser la question un peu étrange : les individus ont-ils des préférences de densité résidentielle ? Et cette préférence est-elle identique au sein de toutes les catégories socio-économiques ? Il est peu vraisemblable que les individus se posent ces questions sous cette forme : ils font leur choix de résidence en arbitrant entre de multiples critères, de multiples contraintes, et en mettant au centre de ce choix le lieu de cette résidence sur une carte, et non en optant pour une densité. Aussi, si un biais d’endogénéité existe, c’est de manière indirecte, parce que la densité est corrélée à des critères importants de choix résidentiels, comme par exemple l’accès à des transports en commun. Pour les catégories qui ne possèdent pas de voiture ou pas de permis de conduire, cet accès est un critère qui a des chances de peser plus fortement sur le choix de résidence. Et inversement, pour ceux qui possèdent une ou plusieurs voitures et déclarent aimer conduire (encore que, sur ce dernier point, on peut se demander dans quelle mesure la nécessité de prendre la voiture altère la psychologie de l’automobiliste). En revanche, est-ce réellement un biais sur la densité ? N’est-ce pas plutôt un biais sur l’accès aux transports en commun ? Il est toujours possible d’ajouter cette dernière variable dans la régression, mais on ne sait pas réellement où arrêter les ajouts. Faut-il ajouter la présence de commerces de proximité ? C’est également un critère important pour celui qui n’a pas de voitures. Puis la présence d’école, etc. Il y a une tentation de réintroduire ici toute la géographie qui a été auparavant écrasée.
Mais revenons à l’équation équation 4. Il peut y avoir un biais d’endogénéité parce qu’il existe une variable cachée qui est liée à la fois à la densité et aux caractéristiques individuelles. Imaginons, par exemple, que le fait d’aimer conduire soit cette variable et que les catégories supérieures aimeraient plus conduire, pour la simple raison qu’ils ont acheté des gros SUV ostentatoires. Dans ce cas, l’estimation effectuée sur les données du tableau réduit n’aboutit pas aux mêmes résultats que les estimations que l’on peut effectuer sur les sous-tableaux définis conditionnellement à une valeur fixée de cette variable cachée. Dans le sous-tableau de ceux qui aiment conduire, on a plus de cadres supérieurs qui habitent loin, dans des zones peu denses, et qui font beaucoup de kilomètres. Dans ce cas, l’élasticité du nombre de kilomètres selon la densité va être fortement négative. Dans l’autre sous-tableau, l’élasticité va être au contraire faiblement négative. Plus problématique, ceux qui aiment conduire ne sont pas allés n’importe où, ils ont choisi d’habiter dans des zones certes moins denses, mais avec une bonne accessibilité en voiture à de nombreuses aménités, dans des zones valorisées, bien entretenues, avec des prix élevés… Ils n’ont pas fait que choisir une zone peu dense mais, encore une fois, certains lieux sur une carte. La forte élasticité observée n’est donc pas un résultat établi sur l’ensemble du territoire observé, mais sur une sélection implicite. C’est ce qui fait que l’on ne peut même pas se contenter d’une estimation moyenne sur les deux sous-tableaux. En réalité, pour des mêmes descripteurs géographiques, une même densité, un même design, il y a des lieux différents sur la carte qui ne sont pas forcément choisis par les mêmes catégories d’individus avec une même appétence à multiplier les trajets en voiture.
La stratégie de modélisation que nous proposons s’efforce au contraire de mener l’analyse en conservant la géographie, sans la réduire a priori à quelques descripteurs synthétiques qui induisent plus de difficultés méthodologiques qu’ils n’en résolvent. Nous estimons chaque composante de l’équation 1 séparément, pour chaque catégorie k d’individu ou de ménage. Chacun des modèles s’efforce d’expliquer un comportement de mobilité – fréquence des boucles, complexité des boucles, choix modal – en mobilisant les données disponibles avec l’idée de pouvoir prédire le comportement d’un individu résidant en un lieu donné. La distance domicile-travail est mobilisée comme variable explicative du comportement, sans que cela pose de problèmes puisque la variable expliquée n’est pas la distance parcourue. Ceci ne signifie pas qu’il ne peut pas y avoir de biais d’endogénéité au sein de ces modèles, mais la stratégie indirecte que nous suivons, en évitant l’exercice de construction de descripteurs géographiques, limite a priori le nombre et la portée de ces éventuels biais.
Nous évitons notamment les interrogations et les biais induits par le tri spatial de la population. En nous efforçant d’expliquer le comportement d’un individu en fonction de son lieu de résidence sur une carte, on évite les difficultés liées à des tris spatiaux spécifiques selon telle ou telle catégorie, tel ou tel descripteur géographique. Les distances parcourues sont estimées en fonction d’une position sur une carte pour une catégorie d’individu ou de ménage. Et ce n’est qu’une fois cette exercice mené à son terme que l’on examine réellement le lien entre la densité ou d’autres descripteurs géographiques et les KVT.
Nous retrouverons la question de l’autosélection et du tri spatial non pas pour estimer le nombre de kilomètres parcourus mais lorsque nous voudrons évaluer la variation de kilomètres que l’on peut attendre d’une modification de la localisation d’un ménage. En effet, l’expérience de pensée qui consiste à changer la localisation d’un ménage ou d’un individu ne peut omettre la question de la vraisemblance de ce scénario : est ce que l’individu ou le ménage acceptent cette localisation ? Ainsi posée la question est cependant bien plus claire. La question de l’acceptation du scénario peut être explicitement débattue, elle peut être favorisée ou imposée que ce soit par des incitations fiscales ou par une réglementation comme le zonage ou l’ouverture de droits à construire limités et localisés. Enfin, les préférences individuelles des ménages qui s’installent n’ont aucune raison d’être celles des ménages moyens que l’on a observé dans une enquête réalisée à une autre époque, dans un autre contexte ou dans un autre endroit et qui consiste à céder au syndrome de l’anecdote dénoncé par Heckman ou Deaton à propos des estimateurs locaux, même sans biais. Ainsi, à défaut de le résoudre complètement, nous pensons largement clarifier la question liée au biais d’endogénéité.
4 Estimations
4.1 Les données : Enquête mobilité, du trajet à la boucle
Pour analyser les pratiques de mobilité des Français, nous nous sommes appuyées sur l’enquête Mobilité des Personnes de 2019. Cette enquête a été conduite par l’INSEE entre avril 2018 et avril 2019 auprès de 13 825 ménages et nous renseigne sur l’équipement en véhicules du ménage et sur les déplacements effectués par un membre du ménage de plus de 6 ans (choisi selon la méthode KISH) au cours d’une journée de la semaine précédent le jour d’enquête. Elle livre une information riche sur les pratiques de mobilité des Français juste avant la grande vague de COVID-19 de 2020 et les confinements. On peut ainsi savoir combien de trajets sont effectués au cours d’une journée, quel est le motif de chacun des déplacements et quelle est le mode de transport utilisé.
Toutefois, derrière l’apparente simplicité des questions posées dans ce type d’enquête se cachent d’importantes difficultés de définition de l’objet. Il n’est en effet pas si simple de définir chacun des trajets et d’y associer de manière univoque un motif de déplacement. Pour ne prendre qu’un exemple, si, en chemin vers mon lieu de travail, je m’arrête pour acheter un croissant, est-ce que je déclare uniquement un déplacement domicile-travail, avec le motif travail, en négligeant l’escale du croissant, considérée comme secondaire, ou bien, est-ce que je déclare deux trajets en considérant que le premier trajet a pour motif d’acheter un croissant ? La difficulté est que cette première partie du trajet, ou ce premier trajet, poursuit plusieurs objectifs. Selon que l’on retient l’un ou l’autre des motifs, on aura des chiffrages très différent du poids de la mobilité des Français pour des motifs professionnels et des motifs alimentaires.
Aussi nous avons adopté la perspective des boucles : une boucle est une série de déplacements qui débute par un départ du domicile et finit par un retour au domicile. Une boucle peut être effectué avec de nombreux motifs. Par exemple, une personne quitte le matin son domicile pour accompagner son enfant à l’école, puis enchaîne en allant directement à son lieu de travail ; le soir, elle prend le temps de faire quelques courses avant de rentrer chez elle. Au cours de cette boucle, les motifs auront été d’accompagner un enfant à l’école, d’aller travailler, de faire des courses et, enfin, de rentrer chez soi. On considère alors que chaque boucle est effectuée pour un motif principal tandis que les autres motifs expliquent les détours et les écarts par rapport à un aller-retour direct entre le domicile et la destination associée au motif principal.
Nous avons retenu quatre grande catégorie de motifs de déplacement : le travail, les études, les courses et, enfin, tous les motifs restants. Et nous les avons hiérarchisés en considérant que certains motifs sont plus impératifs que d’autres et qu’ils constituent en général le motif principal d’une boucle. Le travail est le motif qui domine les autres, suivi des études, des courses et, finalement, tous les autres motifs.
Pour chaque boucle, nous avons aussi retenu un mode de transport principal. Ceci ne pose pas de réelles difficultés car, dans la plupart des cas, il y a unicité du mode de transport tout au long d’une boucle. Si je prends la voiture pour aller au travail, il est très probable qu’au passage j’accompagne mon enfant à l’école en voiture et que, le soir, je fasse un détour en voiture pour faire les courses avant de rentrer à la maison en voiture. En revanche, si j’accompagne mon enfant à pied, avant d’aller rejoindre le métro pour aller à mon travail, nous retiendrons que le mode principal de la boucle est le métro. En 2019, il n’y avait quasiment pas de boucles réellement multimodales, c’est-à-dire de boucles où la personne alterne entre la voiture, les transports en commun ou le vélo.
Les kilomètres parcourus selon EMP 2019
L’enquête mobilité des personnes nous sert de source, conjointement à MOBPRO, et il est est donc utile d’avoir en tête quelques résultats qui seront confrontés aux résultats des simulations. La ville compacte étant une dimension au cœur de notre discussion, il est intéressant de séparer les communes suivant leur densité. Il s’agit ici de la classification de l’INSEE de la « grille communale »5 qui présente les mêmes défauts –- échelle arbitraire, fixe, administrative dans ce cas et donc de taille variable, ne tenant pas compte de l’environnement général –- que ceux évoqués précédemment.
5 https://www.insee.fr/fr/information/6439600
Comme on peut le constater sur le tableau 3, entre une « commune très dense » et une « commune peu dense », il y a un ratio de un peu moins que 1 à 2 pour les kilomètres parcourus annuellement, pour le motif principal travail.
4.2 De la fréquence des boucles
A ce stade, notre objectif est d’estimer la fréquence journalière des boucles à partir des comportements constatés dans EMP 2019. Nous limitons ici notre examen aux boucles effectuées pour le travail, ce pourquoi nous étudions uniquement les comportements des actifs. Par ailleurs, nous avons exclus l’Ile-de-France car les pratiques de mobilités y sont spécifiques (plus de transport en commun) et les résidents s’écartent de la population moyenne (plus de jeunes actifs diplômés). Cela risquerait de produire un effet de composition (Yule-Simpson) qui biaiserait les résultats. La distribution de la fréquence peut être observée à partir d’un rootogram, selon la suggestion de John Tukey (Tukey, 1977). On voit alors sur le graphique figure 2 que cette distribution est moins dispersée que ce que prévoit la distribution « classique » de Poisson. Il y a une forte concentration sur la valeur 1, ce qui ne constitue pas une surprise : la plupart des actifs font quotidiennement une unique boucle domicile-travail. Ensuite, certains font deux boucles, vraisemblablement parce qu’ils rentrent chez eux pour déjeuner. D’autres encore ne vont pas aller à leur travail pour diverses raisons (vacances, maladie, week-end…), mais la fréquence observée est inférieure à ce que prévoit une distribution de Poisson. Enfin, de rares actifs font plus de deux boucles domicile-travail au cours d’une journée. Dans l’ensemble, la distribution est peu dispersée, bien moins qu’attendue dans le cas de Poisson.
Pour tenir compte de cette sous-dispersion, nous avons modélisé cette distribution à partir de la distribution de Conway-Maxwell-Poisson (Conway et Maxwell, 1962), qui ajoute au modèle de Poisson un paramètre pour ajuster la dispersion. Elle s’écrit comme suit :
P(x=n|\lambda,\nu) = \frac{\lambda^n}{Z(\lambda, \nu) \times (n!)^\nu} \quad pour\ n=0,1,2...
avec la constante de normalisation Z(\lambda, \nu) = \sum_{n=0}^\infty \frac{\lambda^n}{(n!)^\nu}. La distribution de Conway-Maxwell-Poisson (CMP) inclut la distribution de Poisson (\nu=1), la distribution géométrique (\nu=0, \lambda<1) ou encore la distribution de Bernoulli (\nu \xrightarrow[]{}\infty) en tant que cas particuliers.
On estime le nombre de boucles journalières liées au travail à partir d’une régression de type Poisson, en substituant la distribution standard de Poisson par celle de CMP. Les variables dépendantes retenues sont la longueur de la boucle, la densité de la commune de résidence et le fait de posséder ou non une voiture. Nous nous en tenons à ces seules variables pour différentes raisons : (i) tout d’abord, nous nous devons d’être parcimonieux pour ne pas démultiplier les temps de calcul (une variable avec N catégories multiplie la quantité de calculs par N) ; (ii) puis on ne retient bien entendu que les variables qui produise un effet ; et (iii), plus encore, on ne retient que les variables qui induisent des différences spatiales. Par exemple, même si la variable sexe peut jouer un rôle au sein de la régression, elle n’a pas de conséquences notables sur la répartition spatiale de la variable dépendante (le nombre de boucles) puisque il y a toujours à peu près autant d’hommes que de femmes dans chaque carreau de résidents.
La spécification du modèle est la suivante pour un individu de catégorie k, sachant que nb^{bcl}_k est le nombre de boucles domicile-travail au cours d’une journée, L^{bcl}_k la longueur moyenne de ses boucles domicile-travail, dens_{res,k} la densité de la commune de résidence et, enfin, voiture_k le fait de disposer ou non d’une voiture.
log(nb^{bcl}_k) = \alpha + \gamma \times log(L^{bcl}_k) + \delta \times dens_{res, k} + \tau \times voiture_k + \varepsilon_k \\avec \\ \varepsilon_k \sim CMP(\lambda, \nu) \tag{5}
| CMP | |
|---|---|
| (Intercept) | 0.272 (0.074)*** <0.001 |
| log(distance) | -0.237 (0.011)*** <0.001 |
| Commune assez dense | -0.022 (0.038) 0.572 |
| Commune peu dense | 0.082 (0.034)* 0.018 |
| A une voiture | 0.211 (0.071)** 0.003 |
| Num.Obs. | 4307 |
| AIC | 8869.5 |
| BIC | 8907.7 |
| Log.Lik. | -4428.767 |
Le tableau 4 présente les résultats des estimations. Le paramètre de dispersion \nu est très significativement différent de 1 et vaut environ 2.2. Il y a bien sous-dispersion de la distribution. Ensuite, comme on peut le voir, la longueur de la boucle joue un rôle négatif, comme on pouvait s’y attendre : plus la distance domicile-travail est importante, moins un actif va envisager de multiplier les allers-et-retours. Disposer d’une voiture fait que l’on hésite moins à faire des allers-et-retours. Enfin, résider dans une commune peu dense conduit un peu plus à multiplier le nombre de boucles.
4.3 Boucles simples ou boucles complexes
Dans la perspective des boucles, les individus ne se contentent pas de faire des allers-et-retours entre leur domicile et leur lieu de travail (boucle simple), mais ils effectuent aussi des détours pour d’autres motifs (boucle complexe). La longueur de la boucle fait alors plus du double de la distance domicile-travail. Du point de vue des individus, c’est un moyen rationnel de minimiser les distances en satisfaisant plusieurs motifs au cours d’un même trajet. Or il se pourrait tout à fait que les individus qui habitent le plus loin de leur lieu de travail soient aussi ceux qui réussissent le mieux à rationaliser les boucles qu’ils effectuent, quitte à ce que ces boucles soient plus complexes. On s’attendrait également à ce que le niveau de vie contraigne à des boucles plus optimisées et qu’au contraire les ménages avec enfants aient plus de contraintes à l’optimisation.
L’examen des données montre tout d’abord que le cas des boucles complexes est relativement marginal : 82% des boucles ayant le travail pour motif principal sont simples. Ensuite, on n’observe pas de fortes différences de comportements selon le niveau de vie.
Nous avons modélisé les détours potentiels en deux étapes. Dans un premier temps, nous avons simplement estimé une régression logistique pour évaluer la probabilité de faire une boucle complexe plutôt qu’une boucle simple. Puis, dans un second temps, nous avons estimé le ratio K de la longueur de la boucle par rapport à la distance domicile-travail. Dans le cas d’une boucle simple, K vaut 2 ; et il vaut 2 ou plus dans le cas d’une boucle complexe.
Commençons par la probabilité d’effectuer une boucle simple. Cette probabilité ne semble pas liée à beaucoup de variables et nous n’avons finalement retenu qu’une seule variable dépendante : le type de ménages.
logit(Prob^{simple}_k) = \alpha + \beta \times typmen_k +\varepsilon_k \\ avec\ \varepsilon_k \sim Binomial \tag{6}
| (1) | |
|---|---|
| Constante | 1.468 (0.134)*** |
| Monoparent | -0.037 (0.213) |
| Couple sans enfant | 0.429 (0.182)* |
| Couple avec enfant(s) | 0.000 (0.151) |
| Autres | 0.593 (0.388) |
| Num.Obs. | 2589 |
| AIC | 2414.0 |
| BIC | 2443.3 |
| Log.Lik. | -1202.012 |
| RMSE | 0.38 |
Comme on peut le constater sur le tableau 5 et comme on pouvait s’y attendre, les ménages avec enfants effectuent plus souvent des boucles complexes.
4.4 Longueur des détours et multiplicateur de distance
Venons-en à l’estimation de la longueur des détours dans le cas des boucles complexes. L’examen des données donne une idée générale de l’allure de la relation entre la longueur du détour et la distance domicile-travail : plus l’on travaille loin de chez soi, plus la part des détours est faible. Autrement dit, plus la distance domicile-travail est importante, plus celle-ci exerce une contrainte à aller « droit au but » si l’on peut dire ; le détour tend vers zéro et la longueur de la boucle tend vers deux fois la distance domicile-travail. Inversement, dans le cas où l’on travaille très près de chez soi, il n’y a plus de contraintes et la longueur de la boucle n’est plus liée à la distance domicile-travail. Dans ce cas, la longueur de la boucle va surtout s’expliquer par les autres motifs, et non par le travail. C’est une limite de l’approche par boucles, qui définit hiérarchiquement un motif principal. Cette limite demeure toutefois moins gênante que les problèmes méthodologiques de l’approche par trajets, qui attribue des longs trajets à des motifs secondaires (comme dans l’exemple précédent le cas de l’arrêt pour l’achat d’un croissant en chemin vers son travail). Ici, le problème est somme toute assez circonscrit : il concerne uniquement ceux qui travaille près de chez eux, lorsqu’ils font des boucles complexes. Et l’erreur tient à un problème d’attribution du bon motif des kilomètres parcourus : il devient erroné de parler de détour au sein d’une boucle travail lorsque ce détour est presque l’essentiel de la boucle. Comme nous le verrons, ce problème pourrait être résolu, si le besoin s’en ressentait réellement, mais il est marginal.
Nous notons ici, de manière simplifiée, L la longueur d’une boucle, d la distance entre le domicile et le lieu de travail, \Gamma la longueur des détours, \gamma la proportion des détours rapportée à la distance domicile-travail et, enfin, K le ratio longueur sur distance. On a les relations suivantes entre ces variables :
L = 2 \times d + \Gamma \\ K = L / d \\ \gamma = \Gamma / d \\ K = 2 + \gamma \tag{7}
On s’attend à ce que K dépende de la complexité de la boucle (plus la boucle est complexe, plus K est grand) et de la distance d (plus la distance est grande, plus K est petit). Le figure 3 illustre ces intuitions en comparant les boucles A et B. L’emploi est plus éloigné dans le cas de la boucle B que dans la boucle A. Le trajet B consiste à faire un détour proportionnellement plus faible pour le motif course ou école. Le facteur multiplicateur K sera supérieur à 2 dans les deux cas, mais devrait être plus grand pour A que pour B (K^A \geq K^B \geq 2).
Le facteur K a plusieurs intérêts dans notre perspective. Tout d’abord, le fait de définir pour chaque boucle un motif principal conduit à attribuer à tort les kilomètres supplémentaires liés aux détours au motif principal. Le facteur K permet d’identifier la part de ces kilomètres supplémentaires et, donc, pourrait permettre de réaffecter ces kilomètres aux autres motifs. Pour l’instant, nous n’avons pas opéré une telle réaffectation : non seulement cela ne changerait les résultats qu’à la marge, mais également nous nous intéressons plus aux kilomètres parcourues totaux qu’aux motifs.
Ensuite, le facteur K ne nous sert pas uniquement pour évaluer l’importance des détours par rapport au trajet direct domicile-travail, mais il nous permet aussi, en sens inverse, d’inférer la distance domicile-travail à partir de la longueur de la boucle. Il se trouve que c’est une difficulté dans l’enquête EMP 2019 : nous connaissons la distance parcourue pour chacun des trajets et, donc, nous pouvons connaître la longueur de chaque boucle effectuée, mais nous n’avons pas d’information directe sur la distance domicile-travail. Nous en sommes réduits à devoir l’inférer.
Heureusement, on peut identifier partiellement le lien entre ces deux distances. Dans le cas d’une boucle simple, le motif principal est le motif de l’aller et le retour a pour motif le bien nommé « retour au domicile ». La distance parcourue est alors de 2 fois la distance domicile-travail (K=2). Dans le cas d’une boucle complexe, il n’est pas toujours possible d’inférer la distance domicile-travail. Ce n’est possible que si le premier trajet de la boucle va directement au travail ou si le dernier trajet revient directement du travail. La figure 3 permet d’illustrer cela. On peut repérer la distance domicile-travail par les trait bleus dans les cas B, C et D. Les boucles B et D sont des boucles complexes, mais telles que le premier ou le dernier trajet sont des trajets domicile-travail. On peut donc poser que la distance domicile-travail est égale à la distance bleue. En revanche, pour une boucle complexe comme la boucle A, où il n’y a pas de trajets directs domicile travail, on ne peut pas déduire la distance domicile-travail, ni le facteur K.
En se limitant aux individus pour lesquels il a été possible d’inférer la distance domicile-travail dans l’enquête EMP 2019, nous pouvons estimer la proportion de détours \gamma en fonction de la distance d. La relation est de type log-log à condition de s’écarter des valeurs nulles, très proches de zéro ou au contraire très élevées. La proportion du détour est parfois nulle, aussi nous avons ajouté systématiquement 1% à cette proportion. Les distances proches de zéro sont également un problème puisqu’elles font diverger la proportion estimée. Or nous voulons un modèle qui renvoie une valeur finie raisonnable quand la distance tend vers 0. Nous avons donc ajouté 1 kilomètre à la distance dans l’équation à cet effet. Cet ajout ne perturbe pas l’estimation pour les longues distances et permet de borner l’effet du multiplicateur à courte distance. Nous avons également écarté les cas où K dépassait 10. Pour ne pas faire trop dépendre nos estimations de ces choix préalables, il fallait utiliser une méthode robuste. Nous avons opté pour une régression par quantile, en estimant la médiane, soit pour des individus indicés par l :
log(\gamma_l) = \alpha + \beta \times log(1 + d_l) + \varepsilon_l \\ avec\ \varepsilon_l \sim \mathcal{N} \\ en\ minimisant \sum_l \left\lvert{\varepsilon_l}\right\lvert \tag{8}
| Coefficient | >5% | <95% | tau | |
|---|---|---|---|---|
| (Intercept) | 1.68 | 1.23 | 2.03 | 0.50 |
| log(distance + 1) | −1.07 | −1.33 | −0.85 | 0.50 |
Le modèle a un R^2 de 0.24. Le graphique figure 4 montre l’allure de notre estimation médiane par rapport aux données issues de l’EMP.
On notera que les détours sont surtout importants – en proportion – à faibles distances et, comme nous l’avons vu précédemment, demeurent assez peu fréquents. L’un dans l’autre, le rôle joué par les détours dans notre modélisation reste relativement modeste.
4.5 Choix modal
A ce stade de notre modélisation des pratiques de mobilités, nous savons prédire la fréquence des boucles et leur longueur. Il reste à estimer les choix modaux des individus en fonction de leurs caractéristiques et des caractéristiques des boucles envisagées. Pour ce faire, nous nous sommes appuyés fort classiquement sur les modèles d’utilités aléatoires (notés RUM par la suite, pour Random Utility Model, McFadden (1974)). Le principe de ces modèles est d’estimer pour chacun des modes de transport disponibles son utilité probable en fonction de divers paramètres comme le temps de trajet, le prix du trajet, le confort ressenti le long du trajet ou encore les caractéristiques de l’individu qui fera le trajet. Une des hypothèses du modèle est que les individus ont des préférences inobservables qui font que leur préférence pour un mode de transport vont varier aléatoirement (du point de vue de l’observateur) d’un individu à l’autre. Ce pourquoi, pour une demande de mobilité donnée, on estime en fait une distribution de probabilités de l’utilité pour chacun des modes. La comparaison des distributions permet ensuite d’estimer la probabilité d’un individu de choisir plutôt tel mode de transport que tel autre mode.
Nous avons estimé deux modèles RUM sur les données EMP 2019 : un modèle avec 4 choix modaux (marche à pied, vélo, voiture, transport en commun) et un autre avec uniquement les 3 premiers choix, pour les cas où il n’y a pas de transport en commun envisageable pour la boucle considérée. Pour mener à bien ces estimations, il faudrait idéalement pouvoir renseigner aux mieux chacun des choix modaux. Or l’enquête EMP nous renseigne essentiellement sur les caractéristiques du trajet effectif selon le mode retenu, et non sur les caractéristiques des modes alternatifs. En conséquence, nous n’avons mobilisé qu’une seule caractéristique spécifique selon le mode : le temps de trajet. Et nous avons dû l’inférer à partir de la vitesse moyenne de chaque mode et de la distance parcourue. Au passage, nous avons fait l’hypothèse que la distance parcourue est indépendante du mode, ce qui n’est pas toujours vérifiée. Même si, sur un territoire donnée, nous pouvons estimer une distance par mode (où, notamment, la distance à pied pourrait être parfois plus courte que celle en voiture), de telles distinctions ne sont pas disponibles dans EMP 2019.
En revanche, s’agissant des caractéristiques partagées entre les différents modes, nous sommes bien moins limités. Nous avons toutefois évacué certaines variables non pas parce qu’elles manqueraient de pertinence, mais parce qu’elles n’induisent pas d’hétérogénéité spatiale. Notamment, le sexe de l’individu peut jouer sur le choix modal, mais le fait d’intégrer cet aspect dans notre modèle n’a pas d’intérêt puisque la distribution spatiale des femmes est similaire à la celle des hommes. Seules nous intéresse les variables qui peuvent engendrer des différences de comportements moyens sur le territoire par effet de composition spatiale. Or, même si les hommes font, par exemple, plus souvent des trajets à vélo que les femmes, cet écart n’a pas de conséquence spatiale puisque la répartition homme-femme est homogène sur le territoire. Nous n’avons pas pris en compte non plus l’âge car nos estimations ont été effectuées sur les actifs uniquement. Certes, il y a bien des différences de comportements de mobilité selon l’âge, mais ces différences s’observent surtout entre les enfants, les étudiants, les actifs et les retraités, plus qu’entre les actifs.
Au final, les modèles RUM estimés s’appuient sur les variables suivantes : U_{bcl,l}^m est l’utilité du mode de transport m pour un individu l prévoyant d’effectuer une boucle bcl, tt_{bcl, m} le temps total des trajets pour parcourir cette boucle dans le mode m, L_bcl la longueur de cette boucle, dens_l la densité de la commune de résidence (selon le code INSEE qui va de 1 pour « Très dense » à 4 pour « Très peu dense », en fusionnant les catégories 3 et 4 car cette dernière est rare dans EMP 2019), typmen_l le type de ménage, voiture_l le fait de posséder une voiture (au moins) et NdV_l le niveau de vie du ménage.
Il s’agit d’estimer les fonctions d’utilités suivantes :
U_l^m = \alpha_m + \beta \times tt_{bcl,m} + \gamma_m \times log(L_{bcl}) + \delta_m \times log(NdV_l) \\ \lambda_m \times dens_l + \mu_m \times typmen_l + \nu_m \times voiture_l + \varepsilon_{m,l} \\ avec\ \varepsilon_{m,l} \sim Loi\ de\ Gumbel \tag{9}
Nous nous en tenons, pour l’heure, à la modélisation la plus simple en faisant l’hypothèse que les erreurs sont distribuées selon une loi de Gumbel, conformément à la première formulation du modèle RUM par McFadden . Ceci revient à supposer que ces erreurs sont indépendantes et homoscédastiques et permet de se ramener à un simple modèle logistique multinomiale.
| Facteur | Coefficient estimé | Ecart type | t Student | p Value |
|---|---|---|---|---|
| (Intercept):car | 3.0 | 1.9 | 1.5 | 0.1 |
| (Intercept):transit | 10.6 | 2.7 | 3.9 | 0.0 |
| (Intercept):walk | 7.0 | 2.2 | 3.2 | 0.0 |
| tt | 0.0 | 0.0 | −2.0 | 0.0 |
| DENSITECOM_RESAssez dense:car | 1.0 | 0.2 | 5.0 | 0.0 |
| DENSITECOM_RESAssez dense:transit | −0.8 | 0.3 | −2.8 | 0.0 |
| DENSITECOM_RESAssez dense:walk | 0.1 | 0.2 | 0.4 | 0.7 |
| DENSITECOM_RESPeu dense:car | 0.5 | 0.2 | 2.3 | 0.0 |
| DENSITECOM_RESPeu dense:transit | −3.1 | 0.7 | −4.4 | 0.0 |
| DENSITECOM_RESPeu dense:walk | 0.1 | 0.3 | 0.3 | 0.8 |
| ldistance:car | 0.7 | 0.1 | 5.0 | 0.0 |
| ldistance:transit | 0.7 | 0.1 | 4.9 | 0.0 |
| ldistance:walk | −1.3 | 0.1 | −11.6 | 0.0 |
| TYPMEN5Monoparent:car | −0.8 | 0.3 | −2.8 | 0.0 |
| TYPMEN5Monoparent:transit | −0.4 | 0.4 | −1.1 | 0.3 |
| TYPMEN5Monoparent:walk | −1.2 | 0.3 | −3.6 | 0.0 |
| TYPMEN5Couple sans enfant:car | −0.4 | 0.3 | −1.4 | 0.2 |
| TYPMEN5Couple sans enfant:transit | 0.0 | 0.4 | 0.1 | 0.9 |
| TYPMEN5Couple sans enfant:walk | −0.8 | 0.3 | −2.9 | 0.0 |
| TYPMEN5Couple avec enfant(s):car | −0.3 | 0.2 | −1.5 | 0.1 |
| TYPMEN5Couple avec enfant(s):transit | −0.1 | 0.3 | −0.4 | 0.7 |
| TYPMEN5Couple avec enfant(s):walk | −0.8 | 0.3 | −3.2 | 0.0 |
| TYPMEN5Autres:car | −0.1 | 0.8 | −0.1 | 0.9 |
| TYPMEN5Autres:transit | 1.7 | 0.9 | 1.9 | 0.1 |
| TYPMEN5Autres:walk | 0.0 | 0.9 | 0.0 | 1.0 |
| voitureTRUE:car | 2.4 | 0.3 | 8.0 | 0.0 |
| voitureTRUE:transit | −1.5 | 0.3 | −4.7 | 0.0 |
| voitureTRUE:walk | 0.0 | 0.3 | −0.1 | 0.9 |
| lrevuce:car | −0.4 | 0.2 | −2.1 | 0.0 |
| lrevuce:transit | −1.0 | 0.3 | −3.7 | 0.0 |
| lrevuce:walk | −0.3 | 0.2 | −1.5 | 0.1 |
On peut voir dans le tableau 7 et la figure 5 les estimations du modèle dans le cas où il y a des transports en commun. Le modèle à un R^2 de McFadden de 0.42. Le modèle sans la possibilité de transports en commun n’est pas très différent.
5 Projection du modèle sur l’agglomération de la Rochelle
Nous avons effectué la projection du modèle sur le territoire de La Rochelle au carreau INSPIRE de 200m. La procédure consiste à appliquer l’équation 1 en imputant au carreau 200m les variables nécessaires. Ces variables sont celles qui nourrissent les différents modèles et qui sont répertoriées dans le tableau 2.
Le figure 6 montre, par exemple, l’estimation du nombre moyen de kilomètres parcourus annuellement par un navetteur résidant dans chaque carreau d’habitation. Comme attendu, plus l’on s’éloigne des zones urbanisées, plus ce nombre de kilomètres augmente. Il est d’une certaine manière une traduction chiffrée de la dépendance à la voiture puisque, avec les modèles de comportements, nous avons pris ici en compte l’adaptation des comportements due à l’éloignement aux emplois.
En appliquant un ratio émissions de CO2 aux kilomètres, on peut construire une carte localisée des émissions de CO2, ainsi que des analyses en variantes. Certains de ces scénarios sont développés dans Lempérière et al. (2023) dans le cadre de l’application à la Rochelle.
5.1 Prix, émission et densité
La carte représentée sur le figure 6 sert de base au figure 7. Chaque point de ce graphique est un point de la carte précédente. La taille du point indique le nombre d’actifs et c’est ainsi proportionnel à la densité, puisque chaque carreau 200m a une taille fixe (4 hectares) ; la couleur représente le prix des transactions immobilières au m² pour l’année 2019 – avec un lissage pour tenir compte du faible échantillonage à cette résolution spatiale. L’axe des y représente les kilomètres moyens parcourus par les actifs de chaque carreau pour leurs déplacements professionnels. Enfin, l’axe des x représente le niveau de vie (c’est-à-dire le revenu divisé par les unités de consommation) moyen des ménages de chaque carreau.
La courbe en gris agrège les différents carreaux en pondérant par la population de chaque carreau et illustre le lien entre kilomètre et niveau de vie. Le nombre de kilomètres est le plus bas pour les ménages les plus pauvres – la contrainte budgétaire les oblige certainement – et les ménages les plus aisés – dont la contrainte budgétaire leur permet de se loger plus facilement près des emplois. Pour les moins aisés, la façon de concilier la contrainte mobilité et la contrainte logement est soit de vivre dans un logement plus petit, soit de se voir solvabiliser par le logement social.
Pour un niveau de vie donné, la dispersion est très grande, mais le lien apparaît significatif pour autant. Les classes moyennes (ni les plus riches, ni les plus pauvres) émettent plus de CO2 en moyenne parce qu’elles vivent plus loin de l’emploi dans des zones moins denses et dont le prix de l’immobilier résidentiel est plus bas. En ce qui concerne les émissions de CO2 liées à la mobilité professionnelle quotidienne, sur le territoire de la Rochelle, notre projection indique que les émissions diminuent avec le revenu sur la partie haute de la distribution des revenus.
5.2 Scénarios de densification
L’intérêt de cette modélisation ne réside pas uniquement dans le fait de pouvoir synthétiser les pratiques de mobilités observées à une maille fine, mais également dans la possibilité de prédire l’évolution de ces pratiques en fonction de certains changements, de certains scénarios de modification urbaine. Ici, pour éclairer le lien entre densité urbaine et émission de gaz à effet de serre, nous avons simulé tout un ensemble de scénarios de densification et estimé les conséquences sur les kilomètres effectués en voiture par les navetteurs.
Chaque scénario a consisté en un petit « choc » démographique –- l’ajout de 100 actifs –- au sein d’un IRIS donné. Comme notre modélisation suppose qu’il y a autant de navetteurs que d’emplois localisés sur le territoire, il fallait également définir comment évoluait la distribution spatiale des emplois. Nous avons considéré que celle-ci croissait de 100 nouveaux emplois répartis à proportion de la distribution initiale. Cette répartition d’emplois ne favorise aucun IRIS en particulier en posant l’indépendance de l’évolution des emplois par rapport aux IRIS. Elle est donc le plus neutre possible (puisqu’elle est correspond à la répartition à l’entropie max) et elle est similaire dans tous les scénarios présentés ici.
On notera que tous les IRIS ne font pas la même taille6. Le choc n’a donc pas le même impact localement et l’on pourrait se demander pourquoi nous n’avons pas plutôt envisagé des chocs migratoires proportionnels à la taille des IRIS. La raison est simple : nous nous intéressons ici avant tout aux conséquences globales, plus qu’à celles très locales, et il fallait donc mener les comparaisons en procédant à un choc de même importance globalement. Nous regardons ainsi comment le territoire « absorbe » ces 100 nouveaux navetteurs en fonction de l’IRIS où ils s’installent.
6 Le plus petit contient 134 actifs, l’iris médian en contient 724, et le plus gros 2338.
On notera également qu’il y a 91 743 navetteurs sur le territoire que nous observons. A cet aune, 100 de plus apparaît comme un petit « choc ». Il fallait vérifier si l’ampleur du choc bouleversait nos résultats et de quelle manière. Aussi avons-nous estimé le modèle avec des chocs plus importants (500, 1000, …), plus faibles (50, 10), voire négatifs (-10, -100). Il se trouve que l’ampleur du choc ne change pas grand chose sur le fond. En effet, notre principal élément de comparaison entre les scénarios est le nombre annuel de kilomètres parcourus en voiture par un résident actif sur le territoire de La Rochelle. Au premier ordre, cette quantité est assez simple à estimer à partir du scénario de référence (figure 6) : si l’on ajoute x individus dans le carreau i alors on peut estimer qu’ils parcourent le nombre de kilomètres typique des résidents de ce carreau i dans le scénario de référence ; il suffit alors de recalculer la moyenne en prenant en compte les kilomètres de ces nouveaux arrivants. Soulignons que cette propriété de quasi-linéarité est une propriété souhaitable de notre modèle : l’ajout de quelques individus ne vient pas perturber les grands équilibres et chacun se comporte à peu près comme les autres résidents de son carreau d’arrivée. Sans cette propriété, le modèle serait instable. Bien entendu, plus l’on rajoute d’individus dans un carreau ou un IRIS, plus notre modèle va finir par faire apparaître des effets non linéaires, en raison notamment de la saturation des emplois de proximité, qui va obliger les nouveaux venus à chercher plus loin un emploi disponible. Et c’est exactement ce que l’on observe. Il reste que, en raison de cette quasi-linéarité, l’ampleur du choc n’est pas un facteur décisif pour estimer les élasticités présentées ici.
On notera enfin que les 100 actifs ajoutés ont à chaque fois les mêmes caractéristiques sociales. Nous avons retenu comme caractéristiques de référence celles du cas majoritaire : des actifs vivant en couple, avec un ou plusieurs enfants, possédant au moins une voiture et ayant le niveau de vie moyen du territoire. Ils ont donc le même modèle de comportements, ce qui ne veut pas dire qu’ils auront au final les mêmes pratiques. Selon les carreaux où ils s’installent, les pratiques seront différentes puisque les comportements s’adaptent à la situation géographique du carreau.
La carte du figure 8 fait clairement apparaître que le nombre de kilomètres parcourus en voiture par les navetteurs sur le territoire varie selon l’endroit où se produit la densification de population. L’élasticité du nombre de kilomètres sur la population totale (soit le ratio de la variation du nombre de kilomètres rapportée à l’ampleur du choc démographique) est négative au cœur de l’aire urbaine, dans le centre de La Rochelle, et devient positive à mesure qu’on s’en éloigne.
Cette carte conforte l’intuition commune qui associe une forte densité urbaine à une réduction des kilomètres parcourus en voiture et, donc, une réduction des émissions de gaz à effet de serre. Il est possible de préciser cette relation en examinant pour chacun des scénarios le lien entre l’élasticité des kilomètres rapportés au choc démographique et l’élasticité de la densité articulée (ou, terme que nous préférons, la densité ressentie) rapportés à ce même choc démographique.
5.3 De la densité aux kilomètres
Le figure 9 montre l’élasticité des kilomètres rapportés au choc démographique et l’élasticité de la densité ressentie rapportée à ce même choc. Nous aurions pu présenter le même graphique avec la densité urbaine au sens usuel mais, dans ce cas, le graphique aurait été simplement moins intéressant puisque l’élasticité de la densité urbaine est une constante dans tous les scénarios. Ce graphique aurait été unidimensionnel en écrasant la dispersion selon l’axe des abscisses. Mais il aurait fourni la même information sur l’élasticité des kilomètres parcourus en voiture sur la population.
Comme on peut le constater sur le figure 9, l’élasticité des kilomètres peut être aussi bien positive que négative. Pour un même choc démographique, une même variation de la densité urbaine, on peut avoir une dégradation du bilan kilométrique ou une amélioration. Une densification – au sens usuel – dans un des IRIS situés en haut du graphique conduit à dégrader le bilan kilométrique. Il s’agit des IRIS correspondant aux communes rurales, celles qui ont été identifiées comme éloignés des emplois. Et, inversement, une densification dans un des IRIS du bas du graphique améliore le bilan kilométrique par actif.
Il est intéressant de relier cette simple analyse aux variations de l’élasticité de la densité ressentie7. On observe tout d’abord que l’élasticité de la densité peut être négative. En effet, lorsque l’on augmente le nombre d’individu dans une zone peu dense, deux effets contradictoires se combinent : d’un côté, on augmente la densité de cette zone, mais d’un autre côté, on augmente la probabilité qu’un individu pris au hasard soit un individu de cette zone peu dense, ce qui a pour effet de diminuer l’espérance de densité. Quand ce deuxième effet domine, la densité ressentie diminue. C’est ce qui se produit pour une partie des IRIS situés en haut du graphique : le choc démographique augmente le nombre de ruraux et diminue la densité ressentie. Pour ces IRIS, le bilan kilométrique se dégrade.
7 La densité urbaine au sens classique se contente de faire une moyenne sur des unités spatiales au lieu de faire une moyenne sur des individus. Or, ce qui nous importe, c’est la densité autour de chaque individu. On peut l’illustrer simplement par le cas de deux unités spatiales où résident 10 individus. La densité urbaine usuelle est de 5 dans tous les cas. Pourtant, ce n’est pas la même chose de se répartir entre les deux unités spatiales en deux groupes égaux de 5 et 5 ou, par exemple, en un groupe de 9 et un de 1. Dans le premier cas, il y a dans chaque unité 5 individus qui cohabitent avec 5 individus (lui compris) : chacun perçoit une densité de 5 et la moyenne est donc de 5. Dans le dernier cas, ce sont 9 individus qui vivent auprès de 8 autres (plus lui-même), et 1 qui vit seul. Cette fois, on a 9 contributions à la densité qui s’élèvent à 9, soit 81, et une contribution qui vaut 1. La densité moyenne est de 8,2. Techniquement, la densité ressentie, c’est l’espérance de densité pour un individu pris au hasard ; la densité urbaine, c’est l’espérance de densité pour une unité spatiale prise au hasard.
Dans le cadran en bas à droite du graphique, on a une autre composante attendue du lien entre densité et KVT : un choc démographique dans un IRIS très urbanisé – ici, le centre de La Rochelle – provoque à la fois une claire augmentation de la densité ressentie et une amélioration du bilan kilométrique par actif.
Il y a enfin un dernier cadran non vide, situé en bas à gauche, où le choc démographique n’a pas d’impact fort sur la densité ressentie tout en améliorant le bilan. Il s’agit de la première couronne autour de La Rochelle. Ainsi, un choc démographique dans cette zone précise a la particularité de ne pas être ressentie comme une densification tout en permettant une forte réduction des émissions de gaz à effet de serre. De nombreux opposants à la densification associent celle-ci à l’image de résidents entassées dans des tours, image qu’ils jugent repoussante. Or ce cadran montre qu’il existe des formes de densification écologique qui ne sont pas ressenties comme des fortes densifications.
Références bibliographiques
Réutilisation
Citation
@article{parodi2024,
author = {Parodi, Maxime and Timbeau, Xavier},
title = {La Ville Compacte, une solution aux émissions de gaz à effet
de serre},
journal = {Document de travail de l’OFCE n°2024-5},
date = {2024-01-30},
url = {https://preview.meaps.fr},
langid = {fr},
abstract = {Le lien habituellement recherché ente densité
résidentielle et émissions de gaz à effet de serre apparaît faible
et on en conclut généralement qu’accroître la densité ne se justifie
pas sous l’angle climatique. Ce lien découle cependant d’une
question mal posée. La forme urbaine peut être un levier important
de réduction des émissions si on prend en compte la distribution
spatiale jointe des résidents et des opportunités. A partir d’une
modélisation des flux entre carreaux par MEAPS, et en la complétant
par une analyse empirique des fréquences de trajets, de complexité
de boucles et des modes de transport pour le motif professionnel,
stratifiée par catégories de ménages, on peut combiner les
informations issues de MOBPRO (le recensement), l’EMP (l’enquête
mobilité des ménages), la localisation des résidents (données
carroyées de l’INSEE), la localisation des emplois (MOBPRO et
fichiers fonciers) ainsi que les réseaux de transport (OSM, GTFS)
pour produire une carte des émissions de
CO\textasciitilde2\textasciitilde{} imputées aux résidents liés aux
déplacements professionnels quotidien.\textless br\textgreater`r
wordcountaddin::word\_count(“trajets.qmd”)` mots.}
}
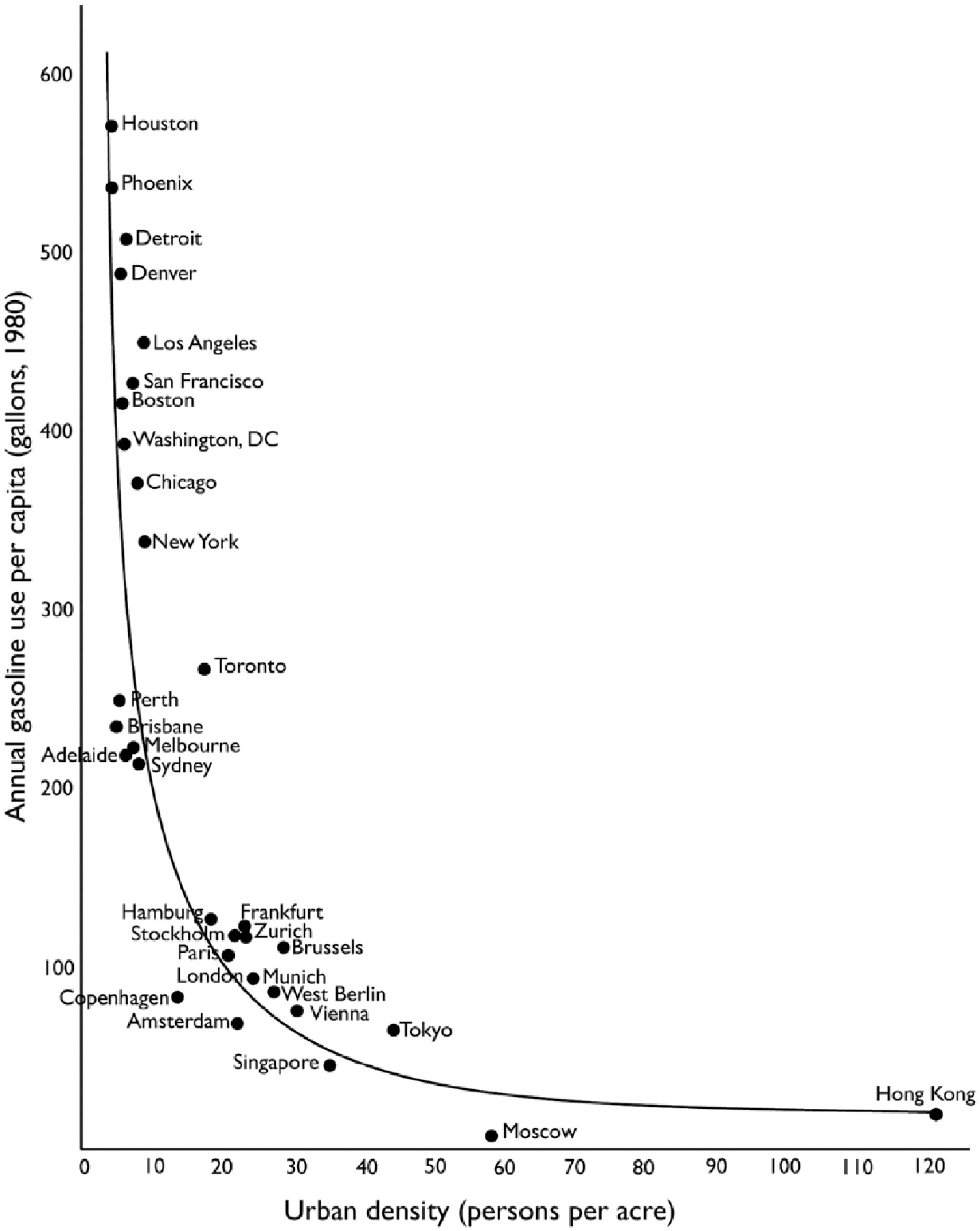
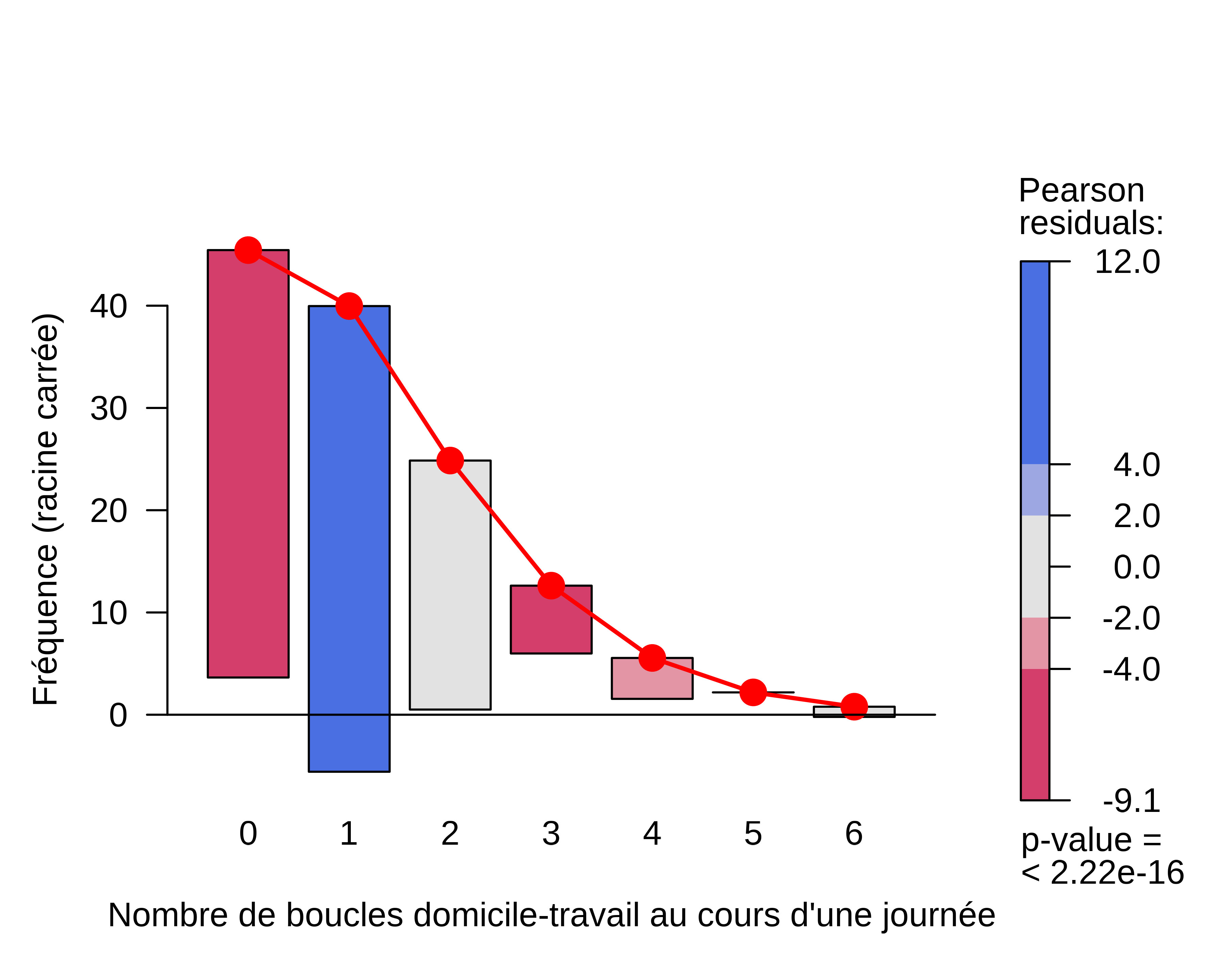
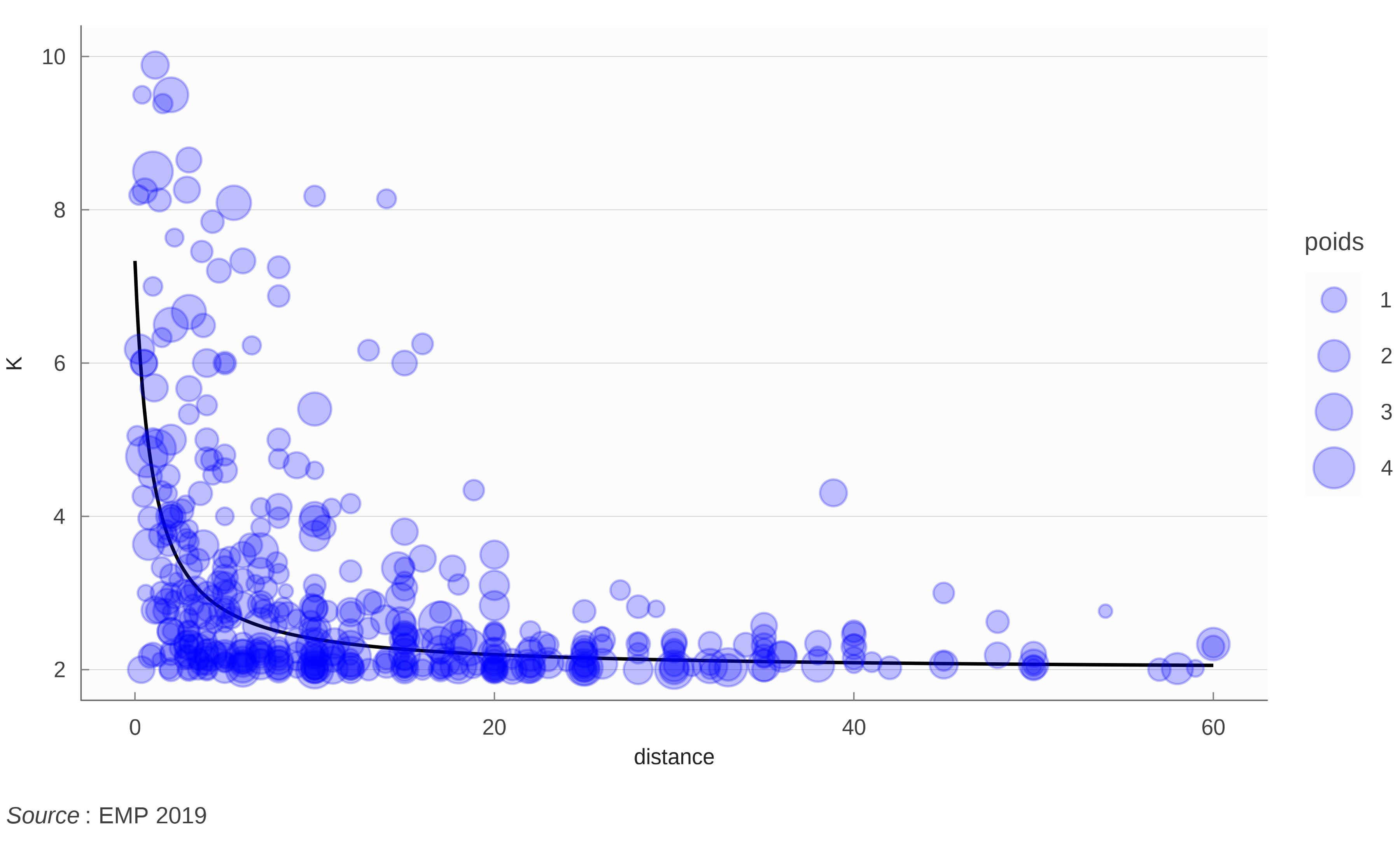
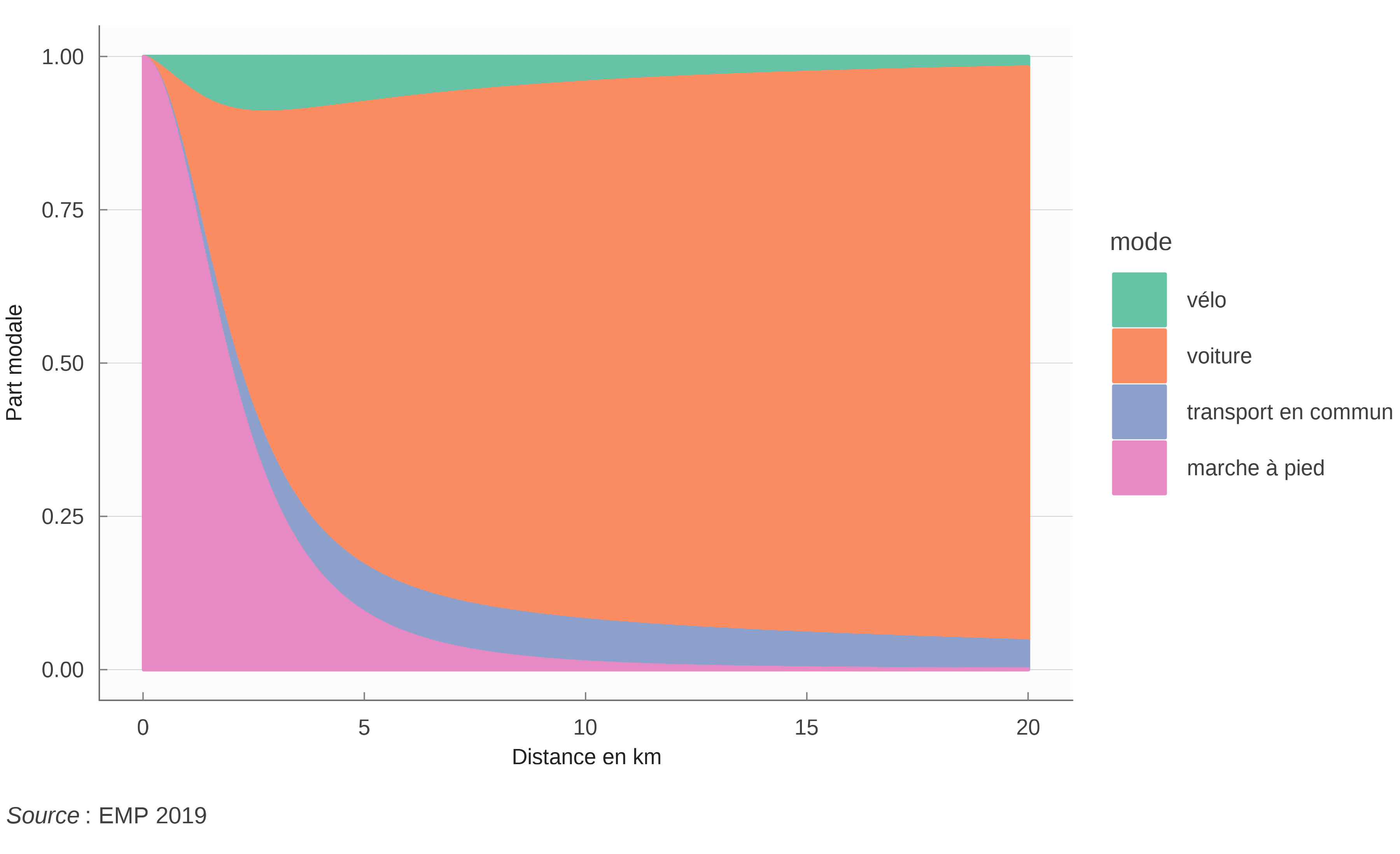


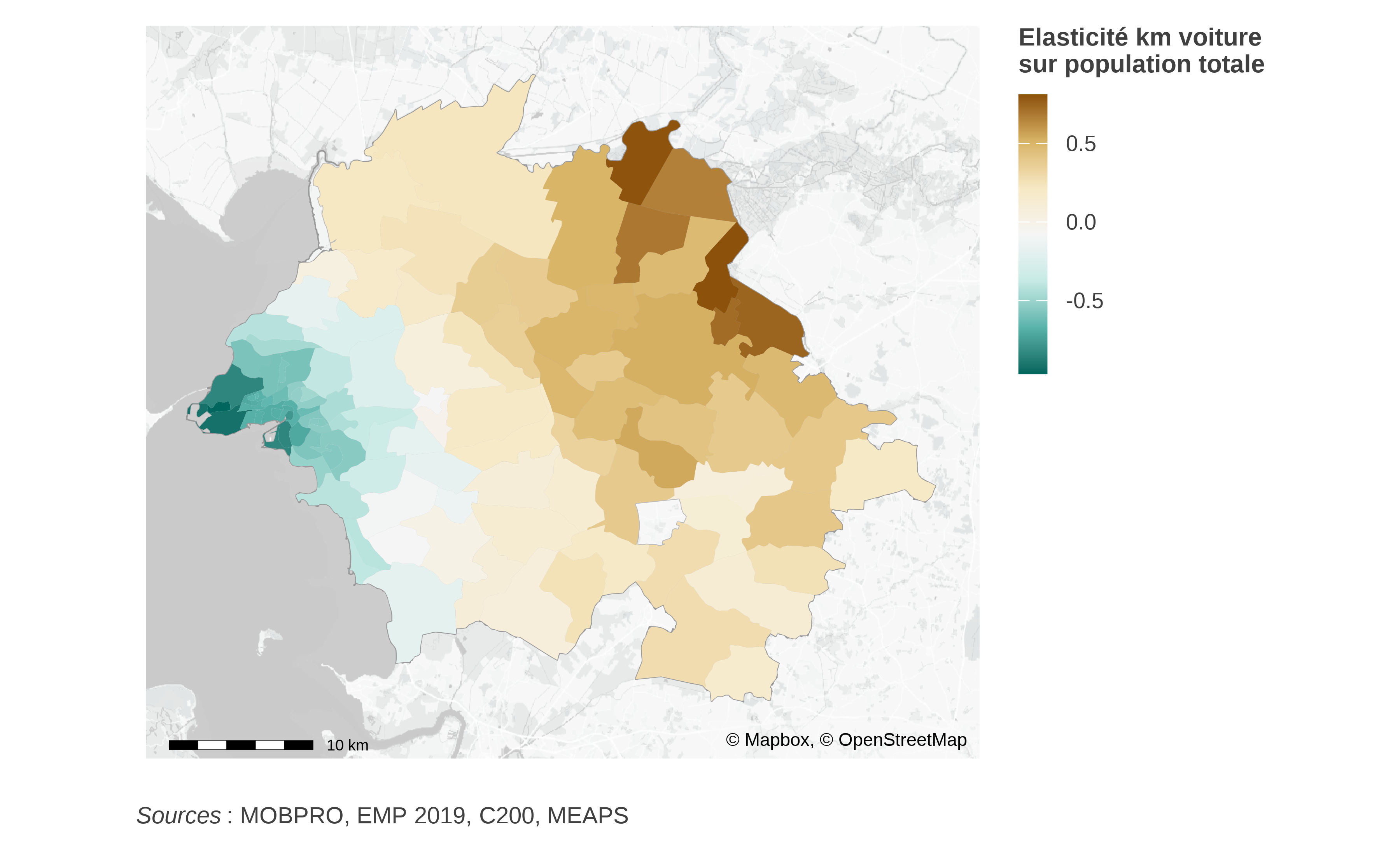
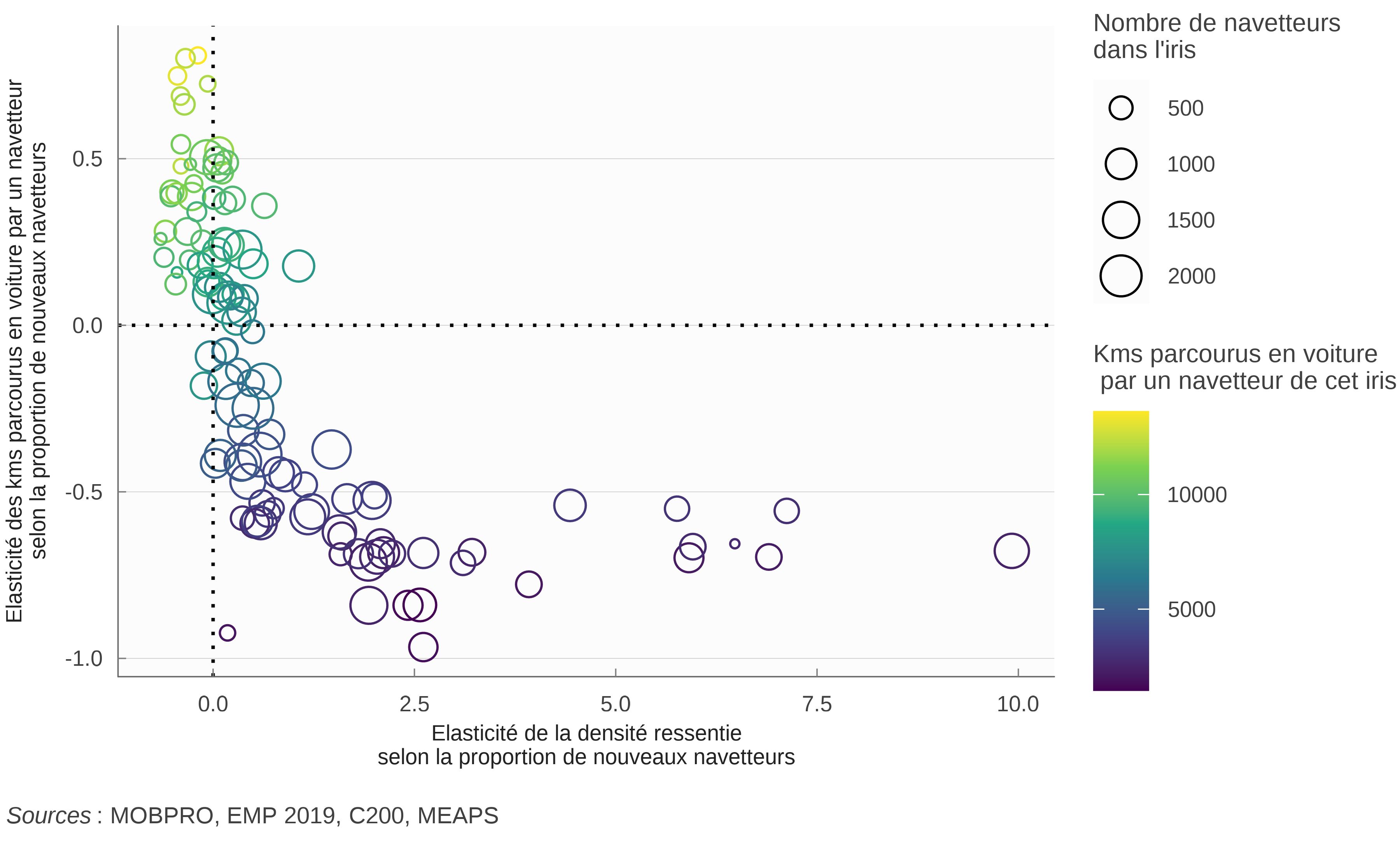
3.2 Comment ? Représentation formelle et stratégie d’estimation
On considère des individus appartenant à des catégories k3 caractérisant leurs comportements de mobilités. Ces individus sont localisés par l’endroit i où ils résident et l’endroit j où ils travaillent. On note alors km^m_{ijk} le nombre de kilomètres parcourus chaque année par un individu de la catégorie k qui réside au carreau i et travaille au carreau j en utilisant le mode de transport m. On se limite ici aux kilomètres parcourus pour des motifs professionnels en considérant que les individus effectuent des boucles domicile_i - travail_j - domicile_i, éventuellement allongées en raisons d’étapes intermédiaires (cf. plus loin).
3 Les catégories k sont construites dans la suite par le croisement de variables catégoriques observées sur les individus (type de ménage, possession d’une voiture, distance au transport en commun par exemple). Le coût en calcul augmente linéairement comme k qui est le produit des nombres de modalités dans chacune des catégories considérées. Ce nombre peut donc augmenter très vite si l’on n’est pas parcimonieux dans la description des individus. Une autre approche serait de dériver les catégories d’une classification distinguant au mieux différents comportements de mobilités.
Pour chaque individu k, km^m_{ijk} se ramène au produit des trois facteurs suivants : (i) le nombre de boucles effectuées par l’individu pour des raisons professionnelles au cours d’une année entre sa résidence i et son lieu de travail j, que l’on note nb^{bcl}_k ; (ii) la longueur typique de chacune de ces boucles, que l’on note L^{bcl}_k ; et (iii) la probabilité qu’une de ces boucles soit effectuée dans le mode de transport m, notée P^{bcl}_{k,m}. Chacun de ces facteurs dépend des caractéristiques k de l’individu et des caractéristiques bcl de la boucle typique passant par i et j. Nous reviendrons plus loin sur les modèles mobilisés pour évaluer ces facteurs. Soulignons, pour l’heure, que le nombre de boucles professionnelles effectuées dans l’année est une fonction des caractéristiques de l’individu et de la distance domicile-travail ou, plus exactement, de la longueur de la boucle typique. Cette longueur de boucle est évidemment une fonction de la distance domicile-travail. Le plus souvent, il s’agit simplement du double (l’aller puis le retour), mais nous tenons compte également de boucles plus complexes, qui allongent le parcours. Nous noterons par la suite K le ratio entre la longueur de la boucle et la distance domicile_travail. K vaut 2 dans le cas des boucles simples, et 2 ou plus dans le cas des boucles complexes. Enfin, le choix modal dépend des caractéristiques des individus et de la longueur de la boucle.
km^m_{ijk} se décompose donc de la façon suivante :
\begin{aligned} km^m_{ijk} & = Nombre\ de\ boucles \times longueur\ d'une\ boucle \times part\ modale \\&= nb^{bcl}_k \times L^{bcl}_k \times P^{bcl}_{k,m} \end{aligned} \tag{1}
Comme nous connaissons la composition sociale de chaque carreau de résidents, le nombre de kilomètres parcourus par un individu moyen résident en i et travaillant en j, noté km^m_{ij}, s’obtient simplement en calculant la moyenne pondérée sur les caractéristiques des résidents en i de l’équation 1. En notant prop_{ik} la proportion de la catégorie k au sein du carreau i, on a :
\begin{aligned} km^m_{ij} &= \sum_k (km^m_{ijk} \times prop_{ik}) \end{aligned} \tag{2}
L’étape suivante consiste à se servir du modèle MEAPS pour calculer km^m_i, soit le nombre de kilomètres parcourus dans l’année pour un individu résident en i dans le mode de transport m. MEAPS nous permet d’évaluer le flux de navetteurs des résidences en i vers les lieux de travail situé en j, flux que nous notons f_{ij}. On peut réécrire ce flux comme une probabilité pour un individu résident en i de travailler en j en divisant par la somme des flux partant de i. Le calcul de km^m_i se ramène alors à un simple calcul de l’espérance mathématique des km^m_{ij} sur l’ensemble de lieux de travail j.
\begin{aligned} km^m_{i} &= \sum_j (km^m_{ij} \times \frac{f_{ij}}{\sum_{j'} f_{ij'}}) \end{aligned} \tag{3}
On notera que, par souci de simplicité, nous avons évalué les flux f_{ij} indépendamment de k, mais il serait tout à fait envisageable d’intégrer cet aspect dans nos estimations.
Le tableau 2 indique les stratégies d’estimation pour chacun des facteurs et la mobilisation des données sources associés à chacun.
4 Les répartitions des destinations entre i et j sont ajustées sur les données MOBPRO. En notant mbp_{IJ} le flux entre la commune d’origine I et de destination J, on a : \sum_{i \in I j \in J}{n_i e_j f_{ij}}=mbp_{IJ}
Comme on peut le constater, il est nécessaire pour poursuivre notre stratégie d’estimation de modéliser les pratiques de mobilités des navetteurs.