MEAPS & gravitaire : estimations à La Rochelle
L’estimation de modèles gravitaires est faite usuellement en utilisant les moindres carrés ordinaires. Nous montrons que la distribution des flux de navetteurs correspond mal à un modèle où l’erreur est log-normale. La représentation par une processus de Poisson, que l’on peut estimer par glm est plus apropriée. A partir de la log-vraisemblance, on remarque que l’estimation par glm est équivalente à la minimisation de l’entropie relative de Kullback-Leibler, ce qui permet l’estimation par minimisaiton non linéaire d’une famille plus grande de modèles, dont MEAPS. La discussion des effets fixes ou aléatoires permet de comprendre en quoi la modélisation respecte ou non les contraintes aux marges du problème. On montre que les modèles qui respectent ces marges peuvent être employés hors échantillon pour prédire les flux de navetteurs. enfin, en utilisant une information infracommunale on peut améliorer la qualité de l’ajustement de MEAPS et produire une intrapolation des flux à une résolution plus importante que celle des données de flux issues du recensement.
12289 mots.
12289 mots.
La confrontation d’un modèle aux données est une étape cruciale pour la compréhension de son fonctionnement et l’appréciation de sa pertinence. Nous explorons ici la capacité du modèle MEAPS à reproduire les flux de mobilités en le comparant au modèle gravitaire. La question est de savoir quel modèle est le mieux à même de reproduire les données observées de flux, à savoir les données MOBPRO tout en introduisant un minimum de paramètres, par souci de parcimonie et de généralité. De plus, cette capacité a expliquer les données doit reposer sur un fondement théorique le plus explicite possible, ce qui est la condition pour pouvoir interpréter les paramètres estimés.
La paramétrisation du modèle, le choix du modèle statistique, ou de la métrique à minimiser pour la détermination des paramètres sont autant de points à clarifier qui dépendent de la nature des données dont on dispose, mais aussi de ce qu’on pense être le processus qui les a générées. Cette discussion est cruciale puisqu’elle peut conduire à des estimations très différentes et qu’il faut expliciter ce qui en fait préférer l’une à l’autre. Elle est également importante pour diagnostiquer la qualité de la modélisation révélée par les données que l’on emploi et nourrir à la fois le processus de modélisation, et la compréhension des données.
Le point de départ est l’estimation d’un modèle gravitaire par les moindres carrés ordinaires (MCO). C’est habituellement ce qui est fait dans la littérature (Josselin et al. (2020) pour la région PACA en France par exemple, Lenormand, Bassolas et Ramasco (2016), Masucci et al. (2013) pour d’autres agglomérations). Mais cette approche mérite d’être approfondie.
1 Spécifications des modèles à estimer
Nous proposons d’utiliser l’entropie relative (ou critère d’information ou log vraisemblance d’une distribution multinomiale) comme fonction objectif à minimiser. Une régression par les moindres carrés ordinaires pondérée par les flux (c’est-à-dire la variable expliquée) donne un résultat plus proche de l’entropie relative que l’erreur quadratique moyenne non pondérée. Nous procédons ensuite à des estimations non-linéaires en utilisant principalement l’entropie relative comme fonction objectif (d’autres fonctions objectifs sont présentées pour comparer). Cette approche permet d’estimer des modèles gravitaires à simple contrainte (la constante c de l’équation 1 n’est plus estimée et est remplacée par un vecteur c_i qui assure le respect de la contrainte en ligne1) et à double contrainte (à la fois la contrainte en ligne et en colonne sont respectées en utilisant par exemple la procédure de Furness). En utilisant la même procédure d’estimation non-linéaire avec comme fonction objectif l’entropie relative, nous estimons également MEAPS étendu afin de permettre une paramétrisation.
1 INfrastructure for SPatial InfoRmation in Europe est depuis 2007 une directive pour la production de données spatialisées. Inspire définit une grille de carroyage et son système de projection harmonisée. C’est ce qui suit l’INSEE dans la diffusion des données carroyées. Voir https://inspire-geoportal.ec.europa.eu pour la définition de la grille et des jeux de données.
Nous déclinons enfin ces estimations en utilisant l’information infra-communale pour montrer que cette information peut accroître le pouvoir explicatif des modèles, en particulier de MEAPS. L’intuition est que l’information infra-communale permet une paramétrisation plus fine que sur la base de l’information communale. Bien que la variable expliquée (les flux) soit connue à l’échelle communale, l’injection d’une information infra-communale permet d’augmenter le pouvoir explicatif des modèles utilisés, particulièrement pour MEAPS.
1.1 Le modèle gravitaire standard : erreurs log-normales
L’estimation de modèle gravitaire est habituellement faite par une régression linéaire (Masucci et al., 2013 ; Lenormand, Bassolas et Ramasco, 2016 ; Josselin et al., 2020), par les moindres carrés ordinaires. Le modèle suivant est celui estimé, où les flux observés f_{ij} sont la variable expliquée et les emplois e repartis dans J unités spatiales, les actifs n répartis dans I unités spatiales et la matrice de distance2 [d_{ij}] sont les facteurs explicatifs :
2 Nous avons pour simplifier l’exposition choisi une fonction « distance » particulière, paramétrée par \delta, appelée fonction puissance avec la forme 1/d^\delta. Des alternatives sont possibles comme la fonction exponentielle, écrite comme e^{-d/\delta}, ou tout autre fonction de la distance, éventuellement paramétrée par plus d’un paramètre. Différentes métriques peuvent être utilisées pour analyser les distances. Cela peut être la distance à vol d’oiseau, la distance de parcours par les réseaux routiers ou le temps de parcours – qui permet d’intégrer les transports en commun. On peut également inclure un coût généralisé de transport, qui découle par exemple d’un modèle de choix discret et qui permet de prendre en compte des notions comme les préférences individuelles pour tel ou tel mode de transport (impliquant des vitesses et donc des temps différents) ou le confort ressenti par un mode de transport, que ce soit pendant le voyage ou par la sécurité qu’il procure dans la faible incertitude de sa réalisation. Nous utiliserons pour l’analyse communale la distance euclidienne à vol d’oiseau. Pour les analyses infracommunales, nous utiliserons des distances et des temps de parcours par les réseaux routiers ou de transport en commune suivant différents modes.
log(f_{ij}) = \alpha \times log(n_i) + \beta \times log(e_j) - \delta \times d_{ij} + c + \varepsilon_{ij} \tag{1}
\varepsilon_{ij} \sim \mathcal{N}(0,\sigma^2)
Ainsi écrit le modèle gravitaire ne respecte la propriété de séparabilité que si les coefficients \alpha et \beta sont égaux à 1. Lorsque \alpha est différent de 1, séparer un groupe de n_i en deux sous groupes, pour lesquels les distances sont inchangées, conduit à projeter des flux dont la somme s’écarte du flux que l’on calcule pour les deux sous-groupes réunis. De façon symétrique, \beta différent de 1 implique la même non séparabilité lors de la séparation d’un groupe e_j en deux. Or cette propriété est nécessaire pour l’utilisation du modèle. Par exemple, la granularité de l’agrégation spatiale ne doit pas trop modifier les flux prévus surtout lorsque cette agrgégation est assez fine pour les distances relatives ne changent pas trop. La séparation des emplois en emplois par secteur, ou des individus suivant des caractéristiques socio-économiques ou suivant leurs préférences est un autre exemple de transformation à laquelle le modèle doit être robuste. Si on sépare les emplois en deux secteurs et que les comportements ne sont pas modifiés le long de cette séparation, il faut que les flux s’additionnent si on suit la cohérence de la modélisation.
Si l’estimation conduit à \alpha\approx\beta\approx1, la propriété de séparabilité sera (approximativement) respectée. Comme nous le verrons dans les estimations, et comme il ressort généralement de la littérature (par exemple Josselin et al., 2020 pour la région PACA), les estimations, en règle générale, du modèle gravitaire par les MCO (i.e. avec des erreurs log-normales) donnent des \alpha et des \beta significativement inférieurs à 1. Le non-respect de cette propriété de séparabilité obère la portée du modèle et sa vraisemblance.
1.2 Quel processus générateur : gaussien ou poisson ?
Le modèle gravitaire log-linéaire estimé par les MCO suppose un bruit multiplicatif et un processus générateur dont les erreurs se compensent. Or les flux s’apparentent plus au résultat d’un comptage qu’au processus implicite du modèle MCO. Les flux ne sont donc plus à considérer comme des erreurs qui se compensent autour d’un modèle déterministe mais comme résultant d’une table de contingence et d’évènements independants mais dont on observe l’accumulation.
Plusieurs représentations sont possibles. Une première approche est de considérer le résultat comme celui d’un tirage avec remise de n boules de différentes couleurs (la dimension i) et placées dans j coupoles aléatoirement. C’est alors une loi multinomiale où chaque cellule de la table a une probabilité \pi_{ij} et les fréquences sont f_{ij} = n \times \pi_{ij} et où n=\sum f_{ij}.
Une alternative, très souvent employée en particulier dans les modèles linéaires généralisés, est de considérer la table de contingence comme produite par des processus de Poisson multivariés Agresti (2002).
Une des propriétés qui différencie ces deux grandes catégories de modèles (multinomial et Poisson versus log normal) se trouve au voisinage des valeurs faibles. Intuitivement, un processus de Poisson a pour variance l’espérance de ce processus. Pour un processus log-normal, la variance est une fonction de l’écart-type et de la moyenne du log du bruit et tend vers une valeur strictement positive lorsque la moyenne du log du bruit tend vers 03. Cette propriété implique que les erreurs relatives pour de petites valeurs dans une représentation log-normale ont une variance plus importante que celle d’un processus de Poisson4.
3 Si log(\varepsilon) \sim \mathcal N ( \mu, \sigma^2), alors Var(\varepsilon) = (e^{\sigma^2}-1)e^{2\mu+\sigma^2}.
4 De façon plus générale, la famille quasi, dans l’estimation par glm, permet de spécifier un lien entre variance et moyenne et ainsi de définir des comportements au voisinage de 0 non pas constant (log linéaire), en lien avec la moyenne (Poisson) mais en carré de la moyenne (Bernouilli) ou en cube de la moyenne. Plus la dépendance est d’un ordre important, plus la variance tend rapidement vers 0.
Une autre façon d’apprécier la différence d’approche entre le modèle log-normal et la table de contingence est à travers la log-vraisemblance. A une constante (indépendante des paramètres à estimer) près la log-vraisemblance pour le modèle log-linéaire est l’erreur quadratique moyenne (msre), en notant \hat f le flux prédit par le modèle et f l’observation :
msre = \sum_i {({log(f}_{ij}) - log(\hat f_{ij}))^2 } \tag{2}
Pour le processus de Poisson, en gardant les mêmes notations, la probabilité des observations connaissant le modèle est :
P(\hat f_{ij}= f_{ij}) = \frac{e^{-\hat f_{ij}}\times \hat f_{ij}^{f_{ij}}}{f_{ij}!} \tag{3}
La matrice de paramètres de Poisson [\hat f_{ij}] peut alors être estimée à partir d’un modèle log-linéaire, qui peut être implémenté facilement par glm. C’est cette approche que Flowerdew et Aitkin (1982) applique à des flux de mobilité. On peut alors écrire le modèle gravitaire simplement :
log(\hat f_{ij}) = \alpha \times log(n_i) + \beta \times log(e_j) - \delta \times d_{ij} +c \tag{4}
On en déduit la log-vraisemblance, en notant n=\sum f_{ij} et en approximant la factorielle par la formule de Stirling (Agresti, 2002) :
\mathcal{L} = -\hat n + \sum_{ij}{f_{ij} log(\hat f_{ij})} - \sum_{ij}{f_{ij}log(f_{ij})} \tag{5}
Dans cette expression, lorsque n est connu (et donc \hat n = n), le processus de Poisson est une loi multinomiale la log-vraisemblance se simplifie par l’élimination de \hat n. Ainsi, la log-vraisemblance pour un processus multinomial est :
\mathcal L = \sum_{ij} f_{ij} log(\hat f_{ij} /n) \tag{6}
L’expression de la log vraisemblance est alors (à une constante indépendante des paramètres près) égale au critère de gain d’information ou d’entropie relative (Kullback et Leibler, 1951) :
I(f_{ij}, \hat f_{ij}) = \frac 1 n \sum_i {f_{ij} \times (log(\hat f_{ij}) - log(f_{ij}))} \tag{7}
Comme l’avaient noté Flowerdew et Aitkin (1982), Sen et Smith (1995) ou encore Griffith et Fischer (2016), les moindres carrés ordinaires reposent sur la minimisation de l’erreur quadratique moyenne, mais les flux de mobilités entre paire de commune ne suivent pas cette distribution (même corrigés par la partie déterministe) et l’estimation est biaisée. Ainsi, quelques paires origine-distribution concentrent la grande majorité des flux alors qu’un grand nombre de paires origine-destination représentent des flux petits et une part cumulée très faible des flux totaux. Dans le cas de la Rochelle et de ses environs, les flux La Rochelle-La Rochelle pèsent presque 20% des flux totaux et les 40 flux les plus importants (sur 2 125) représentent plus de 50% de l’ensemble des flux. L’hypothèse d’un processus générateur multinomial ou Poisson conduit à prendre en compte correctement la possibilité de flux faibles, associés à des paramètres de Poisson petits. Le modèle log-normal donne une trop grande importance aux petits flux, ce qui est d’autant plus problématique que les petits flux sont, de part la nature du problème, très nombreux. Ainsi, la différence entre les métriques (erreur quadratique moyenne versus entropie relative) sera d’autant plus importante que les données que l’on utilise sont très éloignées d’une distribution uniforme ou normale. Cette intuition sera illustrée par la comparaison des écarts observés/prévus des différents modèles que nous aurons estimés. Comme expliqué par (Agresti, 2002, p. pp.146‑148), une alternative à l’erreur quadratique moyenne est de procéder à une régression log-linéaire du type de l’équation 1 mais pondérée par les flux (i.e. l’anti log de la variable expliquée). Dans ce cas la fonction objectif à minimiser est :
msre_w = \sum_i { f_{ij} \times (log(f_{ij}) - log(\hat f_{ij}))^2 } \tag{8}
Nous verrons qu’il existe, outre le carré, une différence entre ce critère et le critère d’entropie relative et qui a trait à la connaissance ou non de la somme totale des flux ou des sommes en ligne ou en colonne. Comme illustré dans la suite pour la Rochelle, le critère pondéré permet des résultats proches de ceux obtenus par glm et Poisson.
1.3 Contraintes en ligne et en colonne
La différence entre le modèle multinomial et le modèle de Poisson tient à la nature de l’information dont on dispose. Pour le modèle multinomial, le nombre total d’individus est fixé, alors qu’il est aléatoire dans le modèle de Poisson. Lorsqu’on passe, dans le modèle de Poisson, des comptes dans chaque case de la table de contingence aux probabilités, ces probabilités suivent une loi multinomiale. Si on connait non seulement le nombre d’individus, mais aussi les marges de la table de contingence (c’est-dire le nombre d’individus pour chaque ligne, ce qui revient à dire que chaque individu occupe un emploi et le nombre d’emplois pour chaque colonne, ce qui revient à dire que chaque emploi est occupé), alors la distribution sous-jacente est hypergéométrique multivariée5. Elle est malheureusement utilisable que pour des dimensions très faibles, par exemple dans le test exact de Fisher (Agresti, 2002).
5 $f(f_{ij}
La formulation simple du modèle gravitaire n’est contrainte ni en ligne, ni en colonne. L’espérance de la somme \sum_j \hat f_{ij} est différente de la \sum_j {f_{ij}}, généralement inférieure du fait de la convexité de la fonction log. Pour approcher ces contraintes, il faut introduire des paramètres supplémentaires, sous la forme d’effets fixes ou aléatoires. Les I contraintes en ligne (appelées aussi simples contraintes, ou contraintes de production des flux) sont représentées en remplaçant la constante c par un vecteur a_i (de taille I) :
\begin{aligned} log(f_{ij}) = & \alpha \times log(n_i) + \beta \times log(e_j) - \delta \times log(d_{ij}) \\ & + log(a_i) + \varepsilon_{ij} \end{aligned} \tag{9}
\varepsilon_{ij} \sim \mathcal{N}(0,\sigma^2)
On peut également le définir comme respectant explicitement les I contraintes en ligne, et donc en tenant compte de la convexité de la fonction log comme écrit dans l’équation 10. L’estimation en peut plus se faire directement par une régression linéaire, puisque le vecteur a_i dépend à la fois de l’estimation de \alpha et de celle de \beta. On peut les estimer par une procédure itérative ou une minimisation non linéaire, dont la fonction objectif pourra être la msre par analogie avec les MCO, l’entropie relative par analogie avec un glm poisson ou la msre_w pour approcher la précédente.
a_i = \frac{n_i}{\sum_j {\frac{n_i ^ \alpha \times e_j ^ \beta} { d_{ij}^{\delta} }}} = \frac{n_i ^ {1-\alpha}}{\sum_j { e_j ^ \beta / d_{ij}^{\delta} }} \tag{10}
Que cela soit par un effet fixe ou aléatoire, dès que l’on introduit le vecteur a_i dans le modèle, il n’est plus possible d’identifier \alpha et on peut supposer pour \alpha n’importe quelle valeur, les a_i étant fonction de \alpha. Le respect de la propriété de séparabilité oblige cependant à choisir \alpha=1. Par l’expression de l’équation 10, le respect des contraintes en ligne induit nécessairement \alpha=1. En effet, log(a_i) peut s’écrire comme la somme de (1-\alpha)log(n_i) et d’un autre terme qui ne dépend que de \beta, e_j, d_{ij} et \delta. L’équation initiale se réduit alors à un terme en log(n_i). Dans le cas du respect des contraintes en ligne, l’élasticité des flux aux actifs est nécessairement unitaire.
Le respect des J contraintes en colonne (appelées aussi contraintes d’attraction) est fait de manière similaire, en introduisant un vecteur b_j. Par le même raisonnement, on ne peut plus estimer \beta et on le fixera à 1, pour respecter la contrainte de séparabilité. Le double respect des contraintes en ligne et en colonne peut se faire par la procédure de Furness (Dios Ortúzar et Willumsen, 2011 ; Griffith et Fischer, 2016) en définissant a_i et b_j comme suit : a_i = \frac{n_i}{\sum_j {{b_j n_i ^ \alpha e_j ^ \beta} / { d_{ij}^{\delta} }}} = \frac{n_i ^ {1-\alpha}}{\sum_j { b_j e_j ^ \beta / d_{ij}^{\delta} }} \tag{11} b_j = \frac{e_j}{\sum_i { {a_i n_i ^ \alpha e_j ^ \beta} / { d_{ij}^{\delta} }}} = \frac{e_j ^ {1-\beta}}{\sum_i {a_i n_i ^ \alpha / d_{ij}^{\delta} }} \tag{12}
Ce dernier modèle, par Furness, peut être estimé par un optimisation non linéaire sans grande difficulté, la procédure de Furness convergeant rapidement. En notant \hat a_i = a_i/n_i^{1-\alpha} et \hat b_j= b_j/e_j^{1-\beta} on a :
\hat a_i = \frac{1}{\sum_j { \hat b_j e_j/ d_{ij}^{\delta} }} \tag{13}
\hat b_j = \frac{1}{\sum_i { \hat a_i n_i/ d_{ij}^{\delta} }} \tag{14}
Ces deux dernières équations montrent que dans le cas de la double contrainte, les paramètres \alpha et \beta disparaissent et le modèle gravitaire se résume à l’équation suivante :
log(f_{ij}) = log(n_i) + log(e_j) - \delta \times d_{ij} + log(\hat a_i) + log(\hat b_j) + \varepsilon_{ij} \tag{15}
L’élasticité de chaque flux f_{ij} aux emplois ou aux résidents est nécessairement unitaire. Cette propriété introduit une différence subtile avec la formulation en effets fixes ou aléatoires dans laquelle les paramètres \alpha et \beta peuvent être fixés à n’importe quelle valeur, les a_i et b_j s’ajustant en fonction. Ceci signifie que dans la formulation effets fixes/aléatoires, le modèle est agnostique quant à la valeur des dérivées à l’augmentation de la masse « actif » ou de la masse « emploi ». L’estimation de \delta est faite en déterminant pour chaque valeur de \delta les flux, auxquels on applique Furness, et donc en calculant les a_i(\delta) et b_j(\delta). On calcule alors la fonction objectif \mathcal{L} pour ces flux (\mathcal{L} étant l’erreur quadratique moyenne ou les autres fonctions objectif) :
\hat \delta = \underset{\delta}{\mathrm{argmax}} \, \mathcal{L}(f_{ij}(\delta)) \tag{16}
Que l’on considère le modèle contraint par Furness ou le modèle augmenté d’effets fixes ou aléatoires, on est face à une difficulté d’interprétation. Indépendamment de leur mode de calcul, les coefficients a_i et b_j agissent comme des modificateurs des masses à l’origine ou à la destination. La partie déterministe du modèle gravitaire peu s’écrire comme l’équation 17 qui fait apparaître à quoi correspondent ces deux coefficients. Pour fonctionner le modèle gravitaire demande de « tricher » sur les masses, ce qui l’écarte de l’interprétation « gravitaire ».
\hat f_{ij} = f_0\frac{(a_i n_i)\times (b_j e_j)}{d_{ij}^\delta} \tag{17}
La solution et l’interprétation proposées par Fotheringham (1983) sont plus intéressantes. Son point est de noter qu’il manque une variable au modèle gravitaire, décrivant le voisinage ou l’environnement de chaque leiu d’intérêt. Suivant son interprétation, les concentrations (des emplois réunis près les uns des autres) pourraient accroître l’attractivité, s’il y a un effet d’agglomération ou au contraire la diminuer s’il y a un effet de congestion ou de recherche de la solitude. Cependant, son approche ne résout pas la questions des contraintes en ligne et en colonne et fait simplement le pari que le problème sera moindre, une fois tenu compte de la concurrence entre opportunité.
1.4 Extension de MEAPS avec des odds-ratios
Pour permettre une spécification plus fine, c’est-à-dire en ajoutant des paramètres, de MEAPS, nous introduisons pour chaque paire (i, j) un paramètre qui modifie la probabilité d’absorption de l’individu i par l’emploi j. On définit c_{abs} comme la chance d’absorption, définie comme c_{abs} = p_{abs}/(1-p_{abs}) . Dans le MEAPS de référence, présenté plus haut, cette chance d’absorption est identique pour tous les emplois considérés par un individu et elle ne dépend que de la probabilité de fuite. Un moyen simple d’injecter de l’information dans le modèle consiste alors à modifier cette chance d’absorption selon les individus et les emplois qu’ils considèrent. Les modifications des probabilités d’absorption peuvent alors être paramétrées par des odds-ratios (des ratios de chances relatives) \omicron_{ij} de telle manière que la nouvelle chance d’absorption de i en j soit égale à \tilde{c}_{abs,ij} = \omicron_{ij} \times c_{abs}. L’odds-ratio \omicron_{ij} est un paramètre entre 0 et +\infty et i et j indexent les communes de départ et d’arrivée. La nouvelle probabilité d’absorption s’écrit alors à partir de la chance d’absorption de référence et de l’odds-ratio comme suit :
\tilde{p}_{abs,ij} = \frac{c_{abs} \times \omicron_{ij}} {1+c_{abs} \times \omicron_{ij}}
Une première stratégie de calage de MEAPS consiste à calculer autant d’odds-ratios qu’il y a de paires communes résidentes - communes d’emplois de manière à reproduire le plus fidèlement possible les flux agrégés de INSEE (2022a). Cette méthode conduit à saturer le modèle puisque l’on estime un nombre de paramètres proche ou égal au nombre de degrés de liberté imposé par INSEE (2022a). Cette stratégie d’apprentissage est analogue à ce qui se fait en machine learning du fait de la démultiplication du nombre de paramètres à estimer. La limite de cette approche est le sur-ajustement (overfitting) qu’elle induit. Celle-ci est habituellement corrigée en ajoutant une pénalité à la complexité du modèle au sein de la fonction d’optimisation. Cela peut également se faire par pruning, en éliminant a posteriori les paramètres dont la contribution à l’explication des données est inférieure à un seuil.
Les paramètres issues de cette approche contiennent une information qui peut ensuite être exploitée. Les odds-ratios s’interprètent alors relativement simplement : ceux qui sont supérieurs à 1 indiquent que le flux de mobilités professionnelles correspondant sont plus fréquents que ce que prévoit le modèle de référence ; et inversement pour les odds-ratios inférieurs à 1.
Une seconde stratégie est une estimation non linéaire. On choisit une structure pour les odds-ratios, en les paramétrisant par une des données disponibles (par exemple \omicron_{ij} = O(d_{ij}), la fonction O étant paramétrisée par un ou plusieurs paramètres \theta. En définissant une fonction objectif (par exemple, l’entropie relative de Kullback Leibler), on peut estimer \theta :
\hat \theta = \underset{\theta}{\mathrm{argmin}} \, \mathcal{L}(f^{meaps}_{ij}(O(d_{ij},\theta)))
2 Données au niveau communal
2.1 Mobilités professionnelles
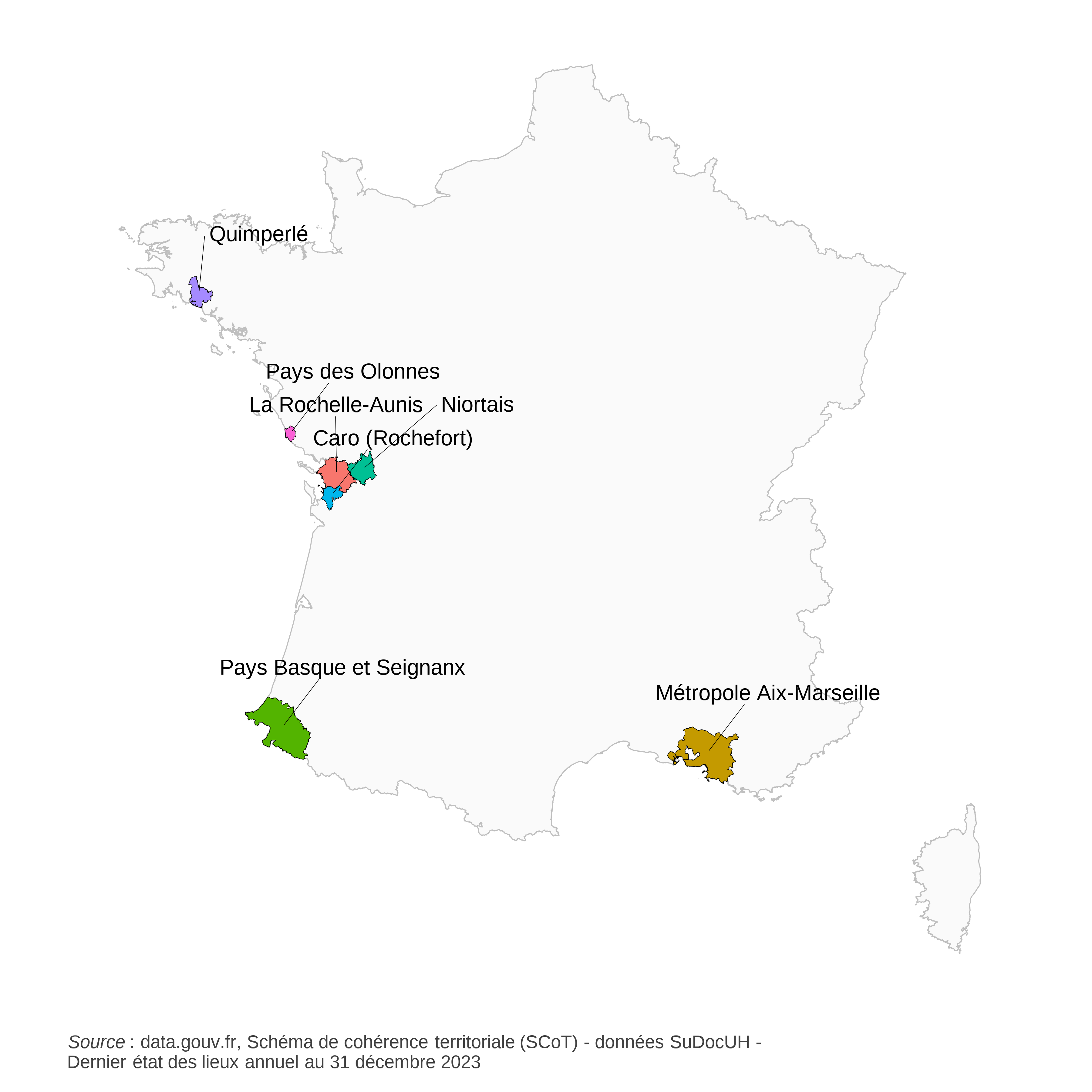
La donnée principale que nous utilisons est issue du fichier détail du recensement. Nous partons de données individuelles, avec une information de localisation à la commune/arrondissement pour la résidence et l’emploi. Les données que nous employons sont issues du fichier détail des mobilités professionnelles de 20206 accessible sur le site de l’INSEE. Nous sélectionnons les individus appartenant à notre territoire d’intérêt : le SCoT de la Rochelle-Aunis pour l’estimation, une sélection d’autres SCoT pour le test, comme illustré sur la figure 1.
6 2020 a été marquée par le COVID. Outre les difficultés à suivre le plan de sondage, on peut estimer que l’analyse des flux de mobilité n’est pas perturbée au premier ordre. En effet, le recensement s’attache à identifier le lieu habituel de travail et de résidence. Les confinements ont probablement limité les changements d’emplois, mais le report d’une partie des relevés de terrain peut en partie compenser cet effet de fixation des emplois.
Le tableau 1 donne quelques statistiques descriptives pour les différents échantillons. La colonne QQ plot indique en particulier que les log des flux ne sont pas normalement distribués avec une masse importante en fin de distribution, ce qui est compatible avec une distribution de Poisson des flux.
| Nombre | distances (km) | fij | log10(fij) | QQ plot de log10(fij) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| actifs | flux | origines | destinations | moyenne1 | écart type1 | moyenne | écart type | part 1% | moyenne | écart type | ||
| La Rochelle-Aunis | 86k | 2195 | 72 | 261 | 11.6 | 11.9 | 39.3 | 203 | 33% | 1.11 | 0.499 |  |
| Métropole Aix-Marseille | 699k | 9775 | 107 | 1310 | 17.6 | 66.9 | 71.5 | 601 | 48% | 1.00 | 0.670 |  |
| Pays Basque et Seignanx | 132k | 4015 | 166 | 729 | 21.5 | 84.6 | 32.8 | 240 | 45% | 0.923 | 0.510 |  |
| Niortais | 50k | 1286 | 40 | 404 | 15.0 | 45.0 | 38.7 | 489 | 53% | 0.922 | 0.494 |  |
| Caro (Rochefort) | 23k | 793 | 25 | 259 | 20.5 | 63.9 | 29.3 | 192 | 41% | 0.939 | 0.471 |  |
| Quimperlé | 21k | 692 | 16 | 210 | 21.0 | 62.7 | 30.6 | 104 | 26% | 1.03 | 0.510 |  |
| Pays des Olonnes | 17k | 326 | 5 | 227 | 19.0 | 71.0 | 52.7 | 537 | 66% | 0.788 | 0.589 |  |
| 1 pondéré par les flux | ||||||||||||
Afin de produire des intervalles de confiance, nous rééchantillonons les données d’estimation (bootstrap). Nous utilisons le fichier détail du recensement, en tirant avec remise les individus du territoire concerné, avec comme probabilité leur poids dans l’échantillon divisé par la somme des poids. Pour les individus ayant des poids proche de 5, lié au plan de sondage du recensement pour les communes de moins de 10 000 habitants, nous les décomposons en 5 individus de poids divisé par 5. Cela permet d’éviter des accumulations autour des multiples de 5 dans la distribution ré-échantillonnée.
Chaque échantillon « boostrapé » a le même nombre d’individus, avec la même distribution, et des individus peuvent être répétés, conformément au principe du boostrap (tirages avec remise).
Nous associons ensuite à chaque paire commune d’origine commune de destination une distance à vol d’oiseau euclidienne entre les centroïdes des communes. Pour les mouvements de la même commune vers la même commune, nous définissons la distance comme la moitié de la racine carrée de la surface. Ceci est une approximation de la valeur moyenne de la distance pour des points répartis aléatoirement sur un cercle de même surface. Dans la partie infra-communale, cette approximation est explicitement levée en localisant au carreau 200m résidents et emplois et en calculant les distances entre toutes les paires origine et destination. Toutes les distances sont exprimées en kilomètres.
Le fichier détail du recensement contient beaucoup de 0 implicites, c’est-à-dire des paires de communes pour lesquelles il n’y a aucun flux. Lorsque les communes sont très distantes, cela se comprend facilement. Mais lorsque l’on analyse un territoire (comme le SCoT de La Rochelle-Aunis), il existe des flux entre communes dont la distance est plus grande que d’autres qui ne sont pas reliées par un flux. Nous avons choisit de traiter comme 0 structurel ces absences de flux, même si l’hypothèse alternative qui voudrait modéliser ces flux presque nuls peut être défendue.
3 Ajustements « communaux » de modèles gravitaires et de MEAPS
3.1 Modèles gravitaires par MCO ou glm
Le tableau 2 donne les résultats d’estimations de différents modèles gravitaires non contraints (i.e \alpha et \beta sont estimés), contraints (i.e \alpha=1 et \beta=1), non pondérés (métrique standard) ou pondérés par les flux en niveau, estimés par glm avec les familles Poisson ou quasi-Poisson, avec effets fixes ou aléatoire ou sans. la forme estimée est l’équation 1 ou l’équation 4, en ajoutant les coefficients a_i et fb_j lorsque des effets fixes ou aléatoires sont ajoutés. Les régressions sont effectuées soit par stat::lm, soit par stat::glm dans R, soit par le package R lme4 pour les effets fixes ou aléatoires. Le tableau présente différentes métriques (voir l’encadré 1 pour les définitions), ainsi que les degrés de liberté des résidus associés à chaque régression.
Dans l’ensemble des régressions, les paramètres estimés sont largement significatifs. La régression par les MCO non contrainte (ligne 1 du tableau 2) fait apparaître des coefficients \alpha et \beta inférieurs à 1, marquant une franche non séparabilité. Contraindre ces 2 paramètres dégrade fortement la qualité de l’estimation (ligne 2), sans pour autant modifier le coefficient associé à la distance. Josselin et al. (2020) estiment pour la région PACA des régressions proches de celle de la ligne 1, avec des R^2 comparables à ceux pour le périmètre de La Rochelle. Le coefficient de la distance qu’ils estiment est entre 0.9 et 1.4, soit nettement au-dessus de celui estimé pour La Rochelle. Ceci suggère que ce coefficient incorpore plus d’information que le simple effet de la distance et résume en partie l’information géographique sur les voisinages qui n’est introduite dans cette régression par aucune variable.
| Modèle | Paramètres | Métriques | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| méthode | p | DL | δ1 | α1 | β1 | R2KLu2 | R2KLi3 | R2dev4 | ||
| 1 | Gravitaire5 | mco | 4 | 2003 | 0.478*** |
0.297*** |
0.399*** |
62.3% | −42.9% | 44.6% |
| 2 | Gravitaire (contraint)6 | mco | 2 | 2005 | 0.5*** |
1 |
1 |
79.0% | 20.5% | 6.3% |
| 3 | Gravitaire (FE)7 | mco | 255 | 1752 | 0.974*** |
1 |
1 |
88.7% | 57.1% | 79.0% |
| 4 | Gravitaire (pondéré)5,8 | mco | 4 | 2003 | 0.933*** |
0.688*** |
0.638*** |
86.0% | 46.8% | 91.3% |
| 5 | Gravitaire (pondéré contraint)6,8 | mco | 2 | 2005 | 0.647*** |
1 |
1 |
79.0% | 20.3% | 20.0% |
| 6 | Gravitaire (pondéré, FE)7,8 | mco | 255 | 1752 | 1.32*** |
1 |
1 |
94.1% | 77.6% | 89.4% |
| 7 | Gravitaire (poisson)5 | glm poisson | 4 | 2003 | 0.93*** |
0.688*** |
0.761*** |
87.1% | 51.2% | 87.1% |
| 8 | Gravitaire (poisson contraint)6 | glm poisson | 2 | 2005 | 0.558*** |
1 |
1 |
79.1% | 20.7% | 20.4% |
| 9 | Gravitaire (poisson, FE)7 | glm poisson | 255 | 1752 | 1.36*** |
1 |
1 |
94.5% | 79.4% | 79.3% |
| 1 estimation du coefficient, entre paranthèse et en italique, erreur standard, entre paranthèse erreur standard calculée par boostrap (128 rééchantillonages avec remise) | ||||||||||
| 2 Entropie relative de Kullback Leibler, normalisé par une distribution uniforme (voir encadré) | ||||||||||
| 3 Entropie relative de Kullback Leibler, normalisé par une distribution indépendante (voir encadré | ||||||||||
| 4 % de la déviance expliquée (voir encadré) | ||||||||||
| 5 log(fij)=αxlog(nij)+βxlog(eij)-δxlog(dij) | ||||||||||
| 6 log(fij)=1xlog(nij)+1xlog(empij)-δxlog(dij) | ||||||||||
| 7 log(fij)=αxlog(actij)+βxlog(eij)-δxlog(dij)+ai+bj | ||||||||||
| 8 Régression pondérée par les flux | ||||||||||
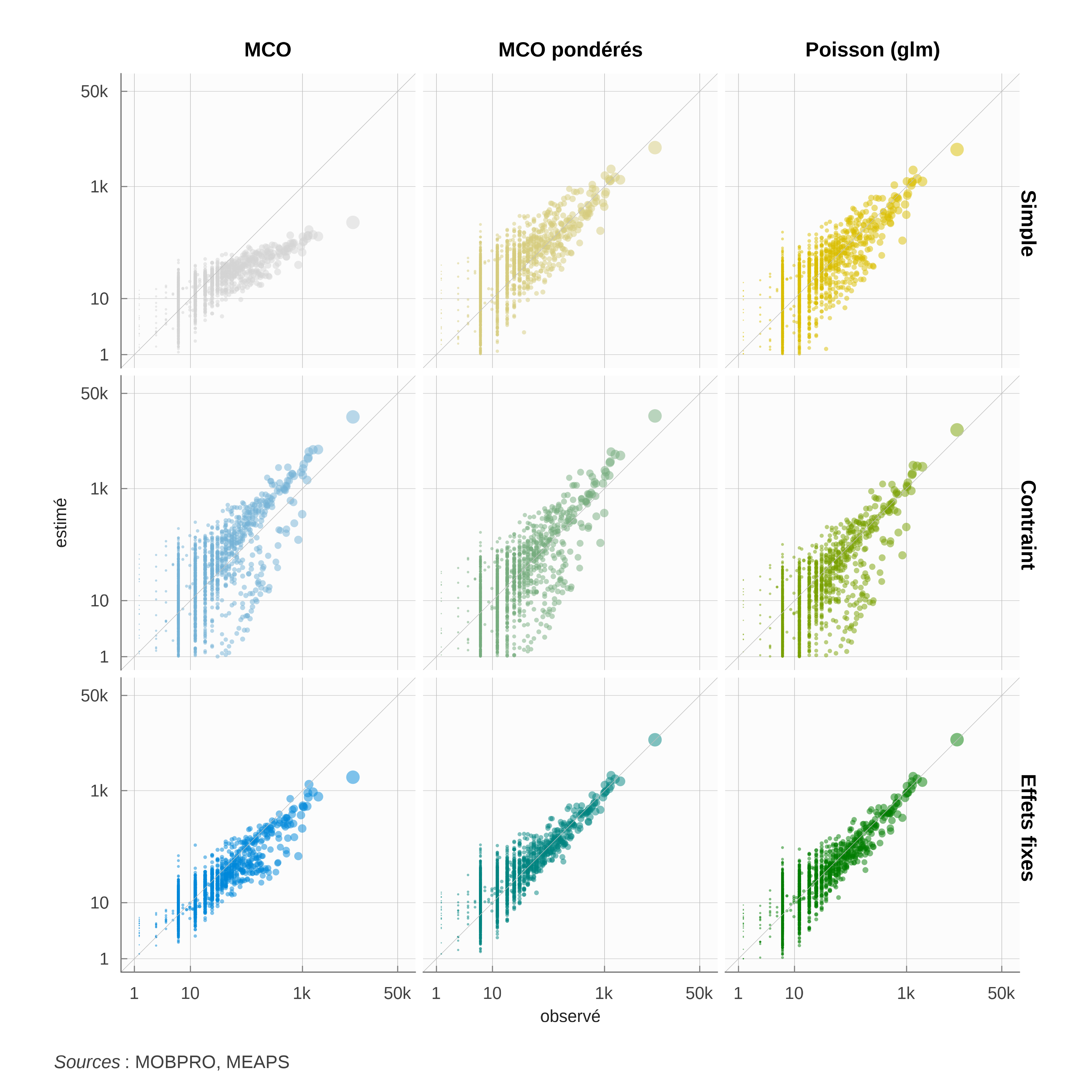
Comme évoqué plus haut, un des aspects problématique des régression par MCO sont le traitement des flux importants. Cet aspect est illustré par le figure 2 où sont représentés les flux observés versus les flux estimés. Les régressions par MCO peinent à estimer le flux le plus important (de la commune de La Rochelle vers La Rochelle). En utilisant la méthode des modèles linéaires généralisés (glm) avec des processus de Poisson résout cette question. La régression de la ligne 7 du tableau 2 illustre ce point. Les graphiques observés versus estimés permettent une appréciation graphique de l’amélioration de l’ajustement. Le biais pour les flux importants est plus faible, la dispersion générale également.
Les coefficients \alpha et \beta sont plus proches de 1, mais pour autant, la propriété de séparabilité n’est pas respectée comme l’illustre la régression contrainte de la ligne 8, pour laquelle la qualité d’ajustement est plus faible. Des estimations par des modèles « quasiPoisson », afin de prendre en compte une éventuelle sur-dispersion par rapport au modèle de Poisson produisent des résultats identiques à ceux par le modèle de Poisson.
Les régressions pondérées par les flux (lignes 4 à 6), dont la fonction objectif est proche du critère de gain d’information ou d’entropie relative, conduisent à des estimations très proches des modèles de des coefficients \alpha et \beta plus élevés. Ils restent néanmoins inférieurs à 1 et lorsqu’ils sont contraints à 1 (ligne 5), l’ajustement, tel que mesuré par le R^2_{dev}, se dégrade nettement. Le coefficient estimé pour la distance dépend assez largement de cette hypothèse, sauf pour l’estimation par les MCO.
En ajoutant des effets fixes ou aléatoires7 pour chaque origine et chaque destination (lignes 6 et 9), et donc un nombre important de paramètres, on améliore la qualité de l’estimation et on force le respect de la propriété de séparabilité en fixant les coefficients \alpha et \beta à 1. Le coefficient de la distance (lignes 3, 6 et 9) est plus élevé et significativement différent de ceux estimés sans effet fixe (autour de 1.3 au lieu d’autour de 1 dans les régressions non contraintes (lignes 1, 4 ou 7)). Comme noté plus haut, si les effets fixes améliorent la qualité de l’estimation, c’est au détriment de l’esprit initial du modèle gravitaire, puisque les effets fixes estimés viennent modifier les masses (actifs et emplois) dans chaque commune pour en assurer l’ajustement. L’utilisation d’effets fixes empêche par ailleurs l’estimation des coefficients \alpha et \beta et oblige à fixer a priori des valeurs. Ainsi, il ets possible d’estimer un modèle à effets fixes avec \alpha et \beta nuls, c’est-à-dire neutralisant l’effet des masses d’origine ou de destination et ne faisant dépendre les flux que des distances entre communes.
7 Seuls les résultats des régressions à effet fixe (communes d’origine et communes de destination) sont reportés dans les tableaux ou des graphiques, les effets aléatoires donnent des résultats très proches. En revanche, pour les prédictions hors échantillon (out of the bag), nous utilisons les régressions à effets aléatoires, les effets fixes n’étant pas connus hors échantillon.
Dans le tableau 2, les écarts type des coefficients estimés sont reportés. Ils sont calculés de deux façons. La première ligne (en italique) est l’écart standard déduit du modèle. Par exemple, pour la ligne 1, il s’agit de l’écart standard pour chaque coefficient pour les MCO, c’est-à-dire en considérant que les résidus sont normaux. En dessous, l’écart type estimé par rééchantillonage (boostrap) est calculé directement sur l’échantillon des coefficients estimés sur les observations rééchantillonées. Pour les estimations par MCO, ces deux écarts type diffèrent fortement, ce qui remet en cause l’hypothèse de normalité des résidus et le modèle choisi. En revanche, pour les modèles estimés par glm et avec un processus générateur suivant une distribution de Poisson, on a bien proximité des écarts type par les deux méthodes.
Le tableau 3 présente les biais d’agrégation pour chacun des modèles estimés. Le biais d’agrégation du modèle gravitaire provient de ce que e^{E(log(\hat f_{ij}))} \neq E(\hat f_{ij}) \neq E(f_{ij}). Or le modèle gravitaire, dans sa forme log-linéaire, ne garantit que l’égalité des espérance des log. Il s’en suit, du fait de la convexité de la fonction log, un biais. La colonne « biais total » illustre l’ampleur de l’écart entre la somme des flux prédits et la somme des flux observés. Cet écart dépasse 60% pour le modèle gravitaire simple et 150% pour le modèle contraint. La pondération par les flux dans les régressions réduit le problème, mais seul la formulation en glm avec un processus de Poisson ramène ce biais à 0. En effet, par cette modélisation E(\hat f_{ij}) = \hat f_{ij} ce qui assure la bonne agrégation des flux prédits.
| R2dev | No | Ne | |No-Ne|/No | Ligne1 | colonne2 | ||||
|---|---|---|---|---|---|---|---|---|---|
| sse/No | sse(1%)/No3 | sse/No | sse(1%)/No3 | ||||||
| 1 | Gravitaire | 45% | 84 953 | 31 778 | 63% | 40% | 26% | 40% | 40% |
| 2 | Gravitaire (contraint) | 6% | 84 953 | 214 622 | 153% | 100% | 74% | 100% | 99% |
| 3 | Gravitaire (FE) | 79% | 84 953 | 51 271 | 40% | 22% | 20% | 22% | 22% |
| 4 | Gravitaire (pondéré) | 91% | 84 953 | 114 610 | 35% | 13% | 3% | 13% | 8% |
| 5 | Gravitaire (pondéré contraint) | 20% | 84 953 | 133 313 | 57% | 47% | 40% | 47% | 46% |
| 6 | Gravitaire (pondéré, FE) | 89% | 84 953 | 96 414 | 13% | 2% | 2% | 2% | 1% |
| 7 | Gravitaire (poisson) | 87% | 84 953 | 84 968 | 0% | 9% | 3% | 9% | 7% |
| 8 | Gravitaire (poisson contraint) | 20% | 84 953 | 84 968 | 0% | 13% | 13% | 13% | 12% |
| 9 | Gravitaire (poisson, FE) | 79% | 84 953 | 84 968 | 0% | 0% | 0% | 0% | 0% |
| 1 Le biais agrégé en ligne est (Σi(Σjfo-Σjfe)2)/No | |||||||||
| 2 Le biais agrégé en colonne est (Σj(Σifo-Σife)2)/No | |||||||||
| 3 Biais agrégé pour les 1% plus grands flux observés relatif à No | |||||||||
De la même façon qu’on analyse le biais agrégé total, on peut analyser ce qu’il se passe en ligne ou en colonne. En agrégeant pour chaque commune de résidence les flux prédits partants, on obtient une quantité que l’on peut comparer le nombre d’actifs observés. La mesure proposée est de ramener la somme des écarts pour chaque ligne au carré rapportée au nombre total d’actifs. On procède de même en colonne. Les modèles contraints impliquent un biais agrégé en colonne comme en ligne important, en lien avec le biais agrégé total. L’utilisation d’effets fixes réduit les biais d’agrégation très proche de 0, au total, en ligne et en colonne, comme attendu.
3.2 Estimations non linéaires
L’approche non linéaire permet d’estimer les paramètres de modèles plus complexes que ceux dont la formulation est linéaire. Dans les estimations non linéaires on cherche les paramètres qui minimisent une fonction objectif qui sera soit la somme pondéré des écarts entre les flux observés et les flux prédits (équation 8), soit l’entropie relative de Kullback Leibler (équation 6).
Par cette approche, on estime deux types de modèles gravitaires : un modèle contraint en ligne et un modèle doublement contraint en ligne et en colonne, spécifiés en suivant l’équation 15. Pour chaque valeur \delta du paramètre de la distance, on calcule par itération les \hat a_i ou les \hat a_i et \hat b_j.
Pour MEAPS, on définit une structure des odds-ratios, par exemple o_{ij} = O(d_{ij}), et pour chaque valeur des paramètres, on calcule les flux par l’algorithme MEAPS. On cherche alors les paramètres qui minimisent l’entropie relative.
Que ce soit pour les modèles gravitaires ou MEAPS, les estimations sont répétées sur les observations rééchantillonées afin de pouvoir calculer une distribution de l’ensemble des statistiques et coefficients déterminés à chaque étape. Ceci permet ainsi de calculer des écarts type pour les coefficients estimés.
Les résultats de ces estimations pour les modèles gravitaires sont reportés dans le tableau 4 et dans le tableau 5 pour les différentes structures d’odds-ratios de MEAPS. La structure de ces tableaux est légèrement différente de ceux reportant les résultats par MCO ou glm, puisque, par exemple, on ne peut pas calculer la part de la déviance expliquée.
| Modèle | Paramètres | Métriques | |||||||
|---|---|---|---|---|---|---|---|---|---|
| objectif | p | DL | δ | α | β | R2KLu | R2KLi | ||
| 1 | Grav. (ligne)1 | KL |
3 | 1932 | 1.16*** |
1 |
0.784*** |
90.0% | 62.1% |
| 2 | Grav. (ligne)1 | R2w |
3 | 1932 | 1.05*** |
1 |
0.685*** |
89.2% | 59.2% |
| 3 | Grav. (furness, l&c)2 | KL |
1 | 1752 | 1.36*** |
1 |
1 |
94.5% | 79.3% |
| 4 | Grav. (furness, l&c)2 | R2w |
1 | 1752 | 1.34*** |
1 |
1 |
94.5% | 79.3% |
| 1 log(fij)=αxlog(nij)+βxlog(eij)-δxlog(dij)+ai ; simple contrainte (en ligne) | |||||||||
| 2 log(fij)=αxlog(nij)+βxlog(eij)-δxlog(dij)+ai+bj ; double contrainte (lignes et colonnes) | |||||||||
L’utilisation de la métrique entropie relative de Kullback Leibler (KL) ou les erreurs au carré pondérées donnent des estimations proches. Le modèle gravitaire avec Furness donne les meilleurs résultats d’estimation et conduit à un paramètre de distance très proche de celui obtenu pour le modèle gravitaire à effet fixe estimé par glm et un processus de Poisson. Une nuance importante est que les \hat a_i et \hat b_j sont déterminés à partir des observations du nombre d’actifs et d’emploi par commune et donc peuvent être projetés hors échantillon, dès lors qu’on observe ces marges.
Les estimations de MEAPS sont uniquement réalisées à partir de la métrique KL. A titre de référence, les flux issus d’un MEAPS sans paramètre, et donc calibré uniquement à partir des marges en ligne et en colonne. La capacité prédictive de ce modèle (ligne 1) est moins bonne que des modèles à paramètre (lignes 2 à 5), mais du même ordre de grandeur que les modèles gravitaires sans effet fixe ou aléatoire (tableau 2). Une différence importante avec ces modèles est que à la fois la propriété de séparabilité et l’absence de biais d’agrégation (total, en ligne et en colonne) sont assurés par construction de MEAPS.
Différentes formes fonctionnelles sont envisagées :
Ligne 1 : le modèle est sans paramètre, uniquement ajusté sur les marges observées.
Ligne 2 : un paramètre pour tous les termes diagonaux, c’est-à-dire les flux allant d’une commune de résidence vers cette même commune pour l’emploi. Formellement, \omicron_{i \neq j}=1 et \omicron_{ii} = o. Le paramètre estimé est de 1.06 avec une erreur standard de 0.05.
Ligne 3 : Un paramètre pour toutes les flux de commune à même commune (diagonales) dont la densité est supérieure à un seuil et 1 partout ailleurs. Cette forme comprend donc deux paramètres et le seuil estimé est que l’odds-ratio spécifique est supérieur à 1 (1.17) pour un peu plus de 35% de la population (le seuil s’applique aux communes classées par densité croissante qui comptabilisent plus de 65% avec une erreur standard de 4 points. L’odds-ratio estimé est ainsi supérieur à celui du modèle de la ligne 2.
Ligne 4 : Un paramètre pour la diagonale d’une part et les communes limitrophes de la diagonale d’autre part (soit 2 paramètres). Formellement, \omicron_{ii} = o_d; \omicron_{ij\in \mathcal{V}(i)} = o_v et \omicron_{i, j \neq i, j \notin \mathcal{V}(i)} = 1. Cette spécification n’ajoute pas beaucoup à la ligne 1.
Lignes 5 et 6 : dans ces deux spécifications, les odds-ratios dépendent de la distance entre la commune d’origine et celle de destination, ce qui permet de combiner MEAPS, où c’est le rang pour chaque individu qui différencie les opportunités et une approche à partir de la distance. Ces spécifications ont deux paramètres et la dépendance à la distance est soit linéaire (ligne 6) soit exponentielle (ligne 5). Ces deux spécifications produisent les meilleurs ajustements.
| Modèle | Paramètres | Métriques | ||||||
|---|---|---|---|---|---|---|---|---|
| objectif | p | DL | p1 | p2 | R2KLu | R2KLi | ||
| 1 | MEAPS 0p.1 | - |
0 | 1753 | - |
- |
82.0% | 51.6% |
| 2 | MEAPS (diag)2 | KL |
1 | 1752 | 1.06*** |
- |
88.4% | 56.0% |
| 3 | MEAPS (diag&densité)3 | KL |
2 | 1751 | 1.17*** |
0.649*** |
88.4% | 56.0% |
| 4 | MEAPS (diag&voisin)4 | KL |
2 | 1751 | 1.06*** |
0.962*** |
88.4% | 56.0% |
| 5 | MEAPS (exp. decay)5 | KL |
2 | 1751 | 3.37*** |
0.0567*** |
91.4% | 67.4% |
| 6 | MEAPS (lin. decay)6 | KL |
2 | 1751 | 14*** |
2.75*** |
91.9% | 69.4% |
| 1 oij=1 | ||||||||
| 2 oii=p1 ; oij=1 | ||||||||
| 3 oii= [q(dens)>p2] p1 ; [q(dens)<p2] 1 | ||||||||
| 4 oii=p1 ; oiv(i)=p2 ; oij=1 | ||||||||
| 5 oij=1/dijp1 + p2 | ||||||||
| 6 oij= [dij>p2] 1 ; [dij<p2] p~1 - (p1-1)/p2 dij | ||||||||
L’examen des graphiques observés estimés confirme ce que les métriques indiquent figure 3. Il est à noter, qu’à part le modèle gravitaire contraint en ligne seulement, chacun des modèles estimé par la procédure non linéaire conduit à une prédiction proche de l’observé pour les plus grands flux. La différenciation se fait ensuite sur la capacité en prendre en compte les flux inférieurs à 1 000.
Rappelons que le modèle gravitaire modifié par Furness s’il possède une bonne capacité prédictive (voir également la performance hors échantillon, c’est au détriment de la portée explicative de ce modèle. MEAPS présente l’immense avantage de comprendre la mécanique à l’œuvre, celle qui conduit à ce que les contraintes soient respectées en ligne comme en colonne.
3.3 Performance hors échantillon
Le test de modèles prédictifs hors échantillon est une discipline forte qui révèle de nombreuses propriétés des modèles. Le tableau 6 reporte la métrique R^2_{KLi} du modèle estimé à La Rochelle-Aunis simulé pour les distances et les masses (actifs et emplois) observés sur d’autres SCoT. Sur la plupart des SCoT, les modèles gravitaires font moins bien qu’une distribution indépendante – qui utilise l’information sur les marges. Les modèles estimés par la procédure non linéaire font en revanche systématiquement mieux que la distribution indépendante et obtiennent des scores comparables à celui sur l’échantillon d’estimation. L’information des marges (le nombre d’actifs et d’emplois par commune) assure une bonne capacité prédictive, améliorée par la modélisation puisque la hiérarchie entre les modèles est conservée.
| La Rochelle (estimation) | Métropole Aix-Marseille | Pays Basque et Seignanx | Niortais | Caro (Rochefort) | Quimperlé | Pays des Olonnes | |
|---|---|---|---|---|---|---|---|
| Estimations linéaires | |||||||
| Gravitaire | −42.9% | 10.9% | 13.1% | −211.8% | −56.7% | −3.3% | −800.8% |
| Gravitaire (poisson) | 51.2% | 53.1% | 67.2% | 21.4% | 30.5% | 35.9% | −113.6% |
| Gravitaire (poisson, RE) | 79.4% | 49.0% | 33.3% | −166.5% | −190.4% | −9.9% | −207.9% |
| Estimations non linéaires | |||||||
| MEAPS (diag&densité) | 56.0% | 58.1% | 71.1% | 57.0% | 52.9% | 56.3% | 34.9% |
| MEAPS (lin. decay) | 69.4% | 74.1% | 81.0% | 57.0% | 75.5% | 62.8% | 46.6% |
| Grav. (furness, l&c) | 79.3% | 81.4% | 88.5% | 81.5% | 75.8% | 73.6% | 50.2% |
| La métrique reportée est le R2KLi, l’entropie relative KL ou gain d’information ; référence indépendante (ni et ej connus) pour les flux prédits à partir des distances de chaque territoire | |||||||
4 Ajustements en utilisant une information infra-communale
On dispose d’une information au carreau 200m qui peut être est pertinente pour reproduire les données de INSEE (2022a), bien que celles-ci sont connues entre commune. En effet, on peut localiser les emplois et les résidents plus finement, au carreau, calculer les temps de parcours entre les paires de carreau et injecter cette information géographique dans le modèle. On peut en attendre une meilleure prise en compte des configurations notamment pour les communes voisines. La distance entre les centroïdes peut masquer une densité d’habitation importante à la frontière entre deux communes, on inversement négliger la structure bi-polaire d’une commune et donc des flux qui se répartissent entre deux voisins proches. En utilisant cette représentation géographique à une échelle plus fine, on peut proposer des paramètrisations plus robustes et dont la signification est plus grande.
Cette approche pose généralement un problème difficile d’optimisation algorithmique. Une approche brutale, qui consiste à minimiser une fonction de perte mesurant l’écart entre les flux estimés et les flux observés, se heurte à la grande dimension de l’espace des paramètres. En outre, comme toujours dans ce type d’exercice statistique, l’enjeu consiste à extraire des données disponibles des enseignements généraux en délaissant ce qui relève de la particularité d’un jeu de données. C’est toute la difficulté du surapprentissage (overfitting) que nous avons évoquée.
Une seconde approche, plus parcimonieuse, consiste à définir une forme fonctionnelle pour les odds-ratios ou encore à regrouper les odds-ratios en quelques clusters pour ensuite n’évaluer qu’un petit nombre de paramètres. Ceci suppose de modéliser la structuration des odds-ratios à partir d’a priori sur les dimensions pertinentes.
4.1 Données infracommunales
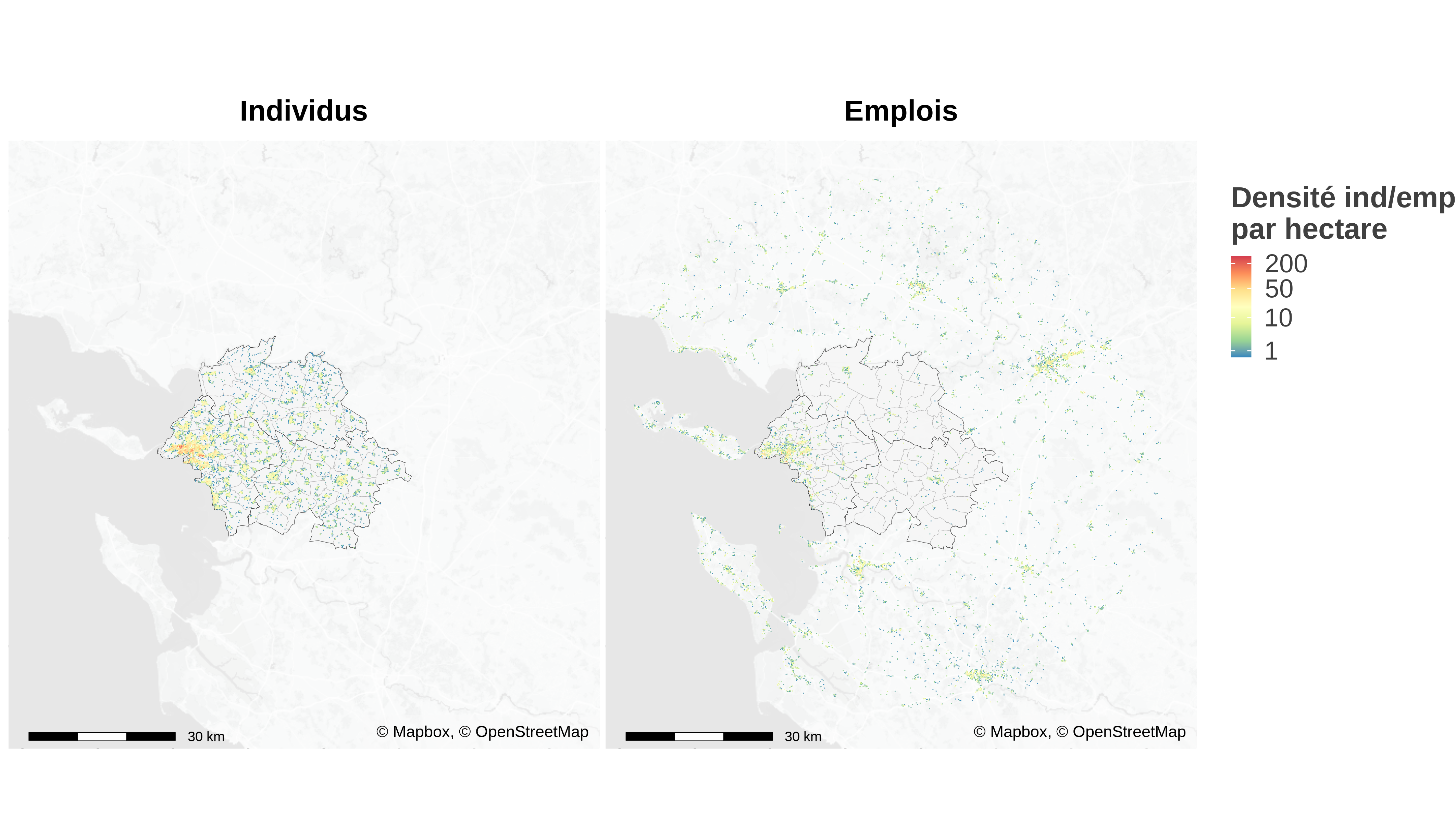
Emplois, résidents au carreau Inspire 200m
La carte de la zone considérée est représentée sur la figure 4. L’analyse est limitée aux résidents du périmètre du Schéma de COhérence Territoriale (SCOT) et considère les emplois dans un rayon 33 kilomètres autour des lieux de résidence. Cette carte est construite à partir des données carroyées de INSEE (2022b) à la résolution du carreau 200m Inspire8. Nous ajoutons à ces données la localisation de l’emploi sur la même grille en utilisant les fichiers fonciers et les données d’emplois localisés de INSEE (2022a). La méthode consiste à imputer par code NAF les emplois de chaque commune selon INSEE (2022a) aux surfaces professionnelles à la parcelle issues des fichiers fonciers. Cela permet ensuite de localiser au carreau 200m les emplois. Cette méthode est assez grossière, puisqu’en particulier la ratio personne/surface n’est pas constant d’une entreprise à l’autre, mais elle fournit une bonne première approximation d’autant que l’extrapolation ne dépasse pas l’échelle de la commune. Elle est en tout cas très supérieure à une imputation uniforme.
8 INfrastructure for SPatial InfoRmation in Europe est depuis 2007 une directive pour la production de données spatialisées. Inspire définit une grille de carroyage et son système de projection harmonisée. C’est ce qui suit l’INSEE dans la diffusion des données carroyées. Voir https://inspire-geoportal.ec.europa.eu pour la définition de la grille et des jeux de données.
Sources : OSM, Mapbox, IGN, carroyage INSEE 2017, Flores et fichiers fonciers 2018
Calcul des distances par mode
Un ingrédient important de l’analyse du territoire est la prise en compte des distances entre chaque paire possible résidence/emploi. Contrairement à l’analyse synthétique, nous ne nous contentons pas de la distance euclidienne.
Pour ce faire nous calculons à partir d’un calculateur d’itinéraire (R5 de Conveyal (Conway, Byrd et Linden, 2017 ; Conway, Byrd et Van Eggermond, 2018 ; Conway et Stewart, 2019) en utilisant le package {r5r} (Pereira et al., 2021) les distances et surtout les temps de transport pour quatre modes (voiture, vélo, transport en commun, marche à pied). Les temps de transport calculés pour chaque paire de carreaux de résidence et d’emploi, en retenant le centre des carreaux, tiennent compte des différentes contraintes de circulation (vitesses limites pour la voiture, sens de circulation, pénalité pour changement de direction, accès autorisé ou restreint suivant le mode, stress à vélo). Concernant les déplacements en voiture, nous ne prenons pas en compte à ce stade la congestion. Concernant les transports en commun, le niveau de détail est assez grand, puisque les fréquences de circulations des véhicules ainsi que les correspondances sont prises en compte. Dans certaines villes, il est possible d’accéder à une information sur les temps de parcours effectifs (mesurant ainsi la congestion ou la disponibilité du réseau) en complément des horaires théoriques. Ces informations ne sont pas disponible pour l’agglomération de la Rochelle et donc cette possibilité n’est pas explorée. L’accès aux données GTFS impose quelques limites, comme par exemple la non prise en compte des réseaux scolaires ou d’autres réseaux locaux ou privés non publiés sous ce format. La modification du réseau de transport comme l’ouverture d’une ligne ou l’accroissement de fréquence est pris en compte en modifiant la matrice des distances et temps par mode entre chaque carreau de résidence et chaque carreau de destination. Dans le cas de l’agglomération de la Rochelle, le nombre de paires calculés est de l’ordre de 16 millions.
A partir des temps de trajets par mode, nous appliquons un modèle de choix discret, Random Utility Model (RUM) à la McFadden, estimé sur l’enquête mobilité des personnes SDES (2021) en utilisant les données de mobilités professionnelles INSEE (2022a) pour caler les flux commune à commune. L’estimation de ce modèle est détaillée dans un autre document (référence à insérer).
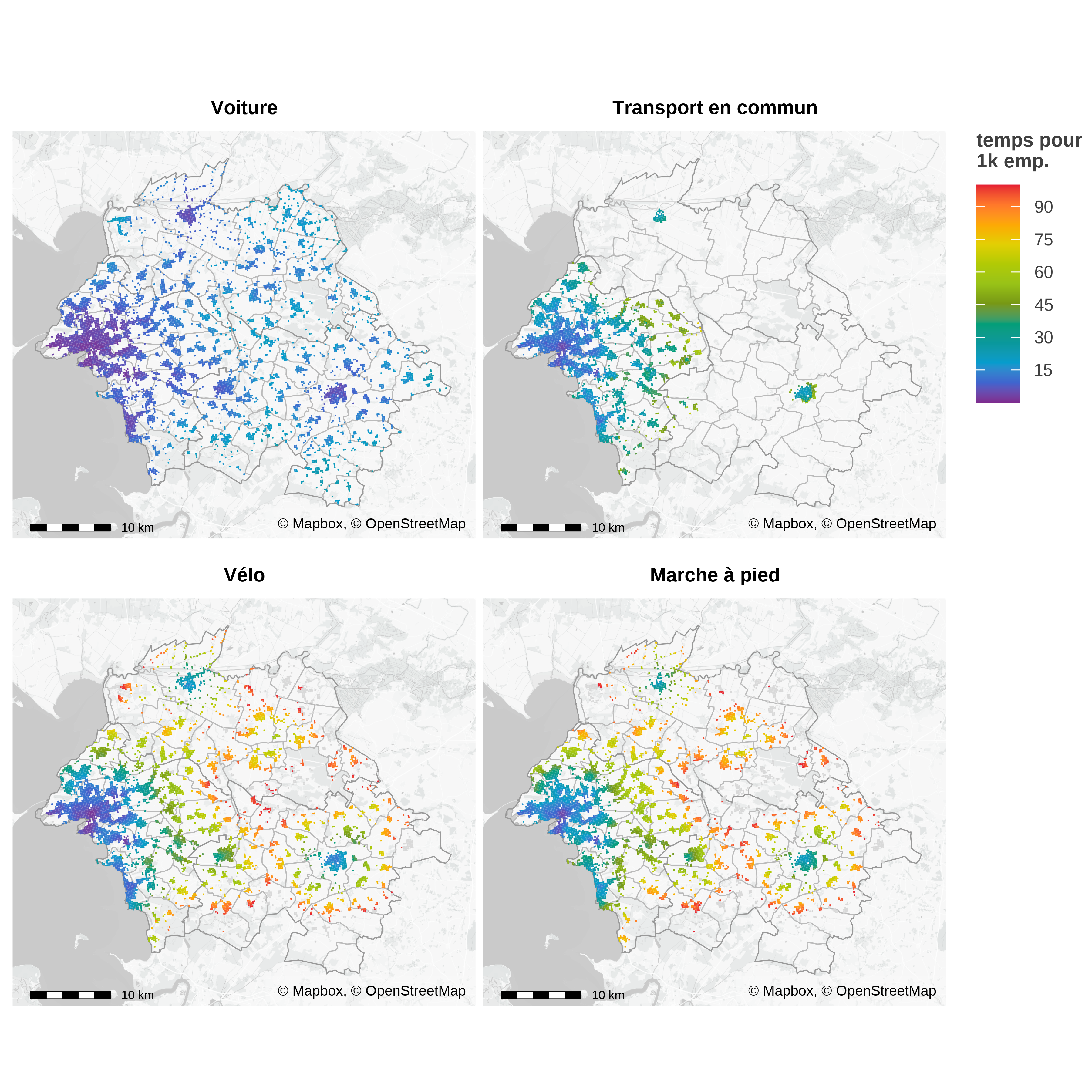
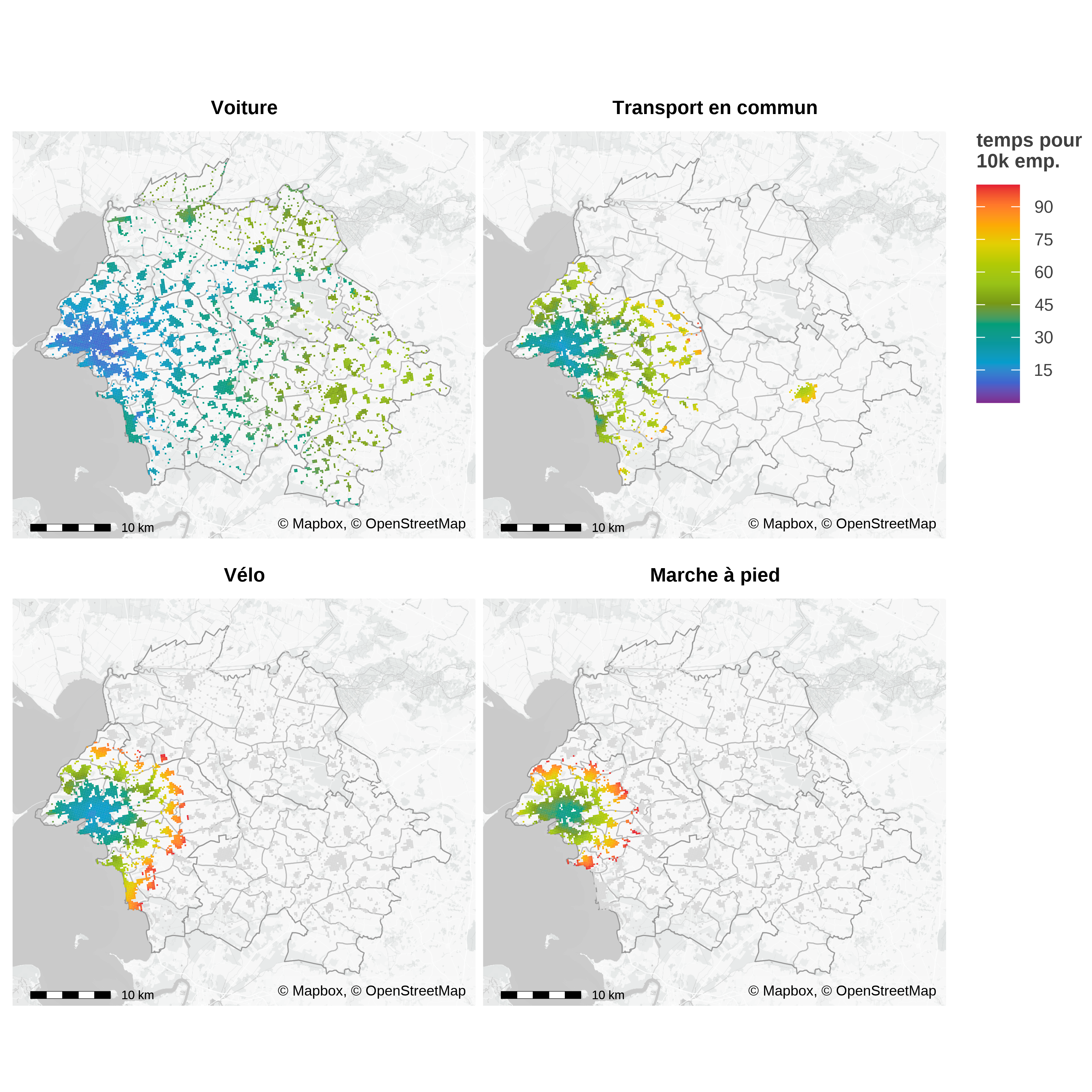
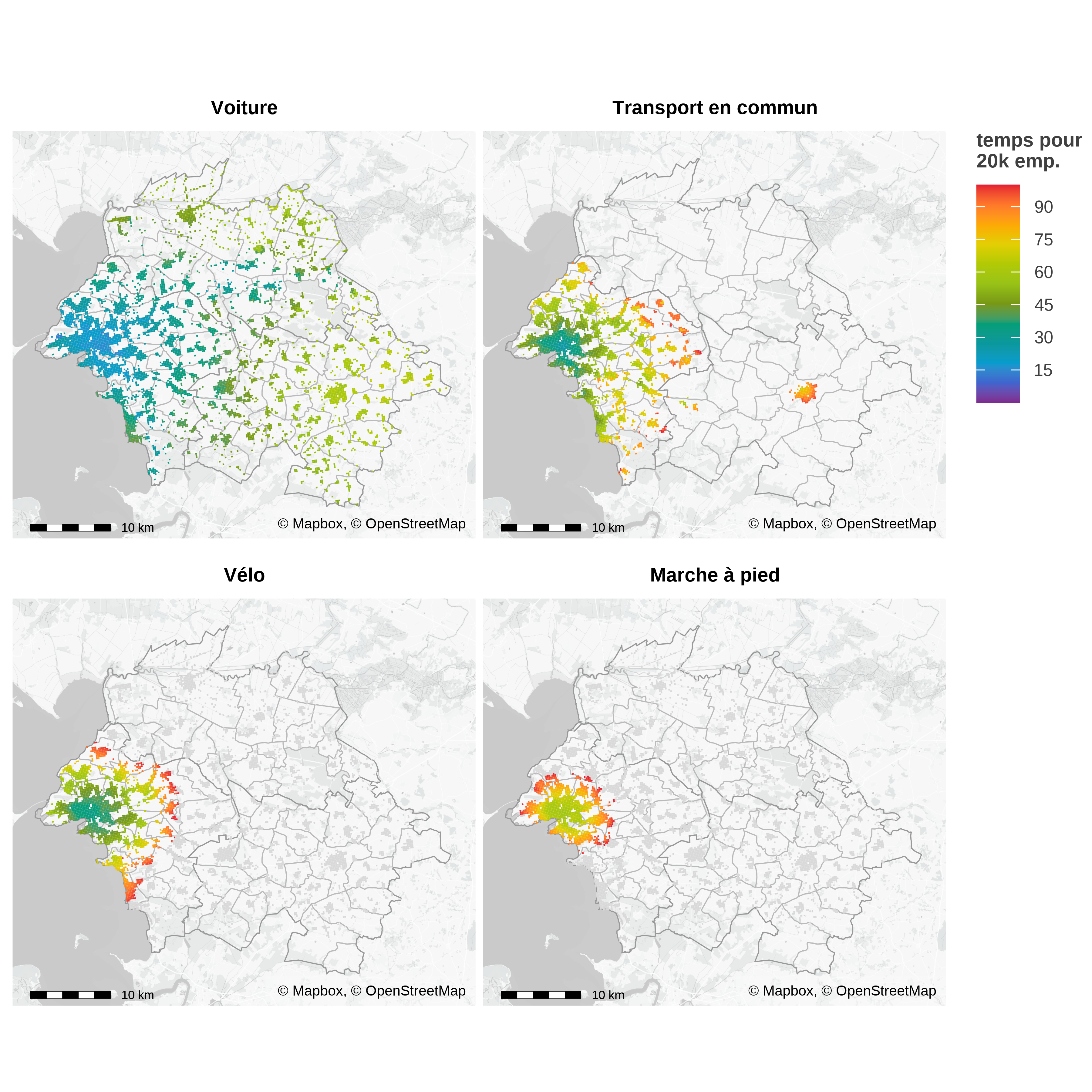
Les distances entre chaque paire de cases permettent de calculer un indicateur d’accessibilité qui joue un rôle central dans le modèle radiatif, et donc dans MEAPS, en remplaçant la distance par la somme des opportunités en deçà d’un seuil de temps. Les cartes du figure 5 représentent les temps pour accéder à un seuil d’emplois en utilisant différents modes de transport.
Calcul des auteurs.
Source : OSM, Mapbox, IGN, Conveyal R5, carroyage INSEE 2017, Flores et fichiers fonciers 2018
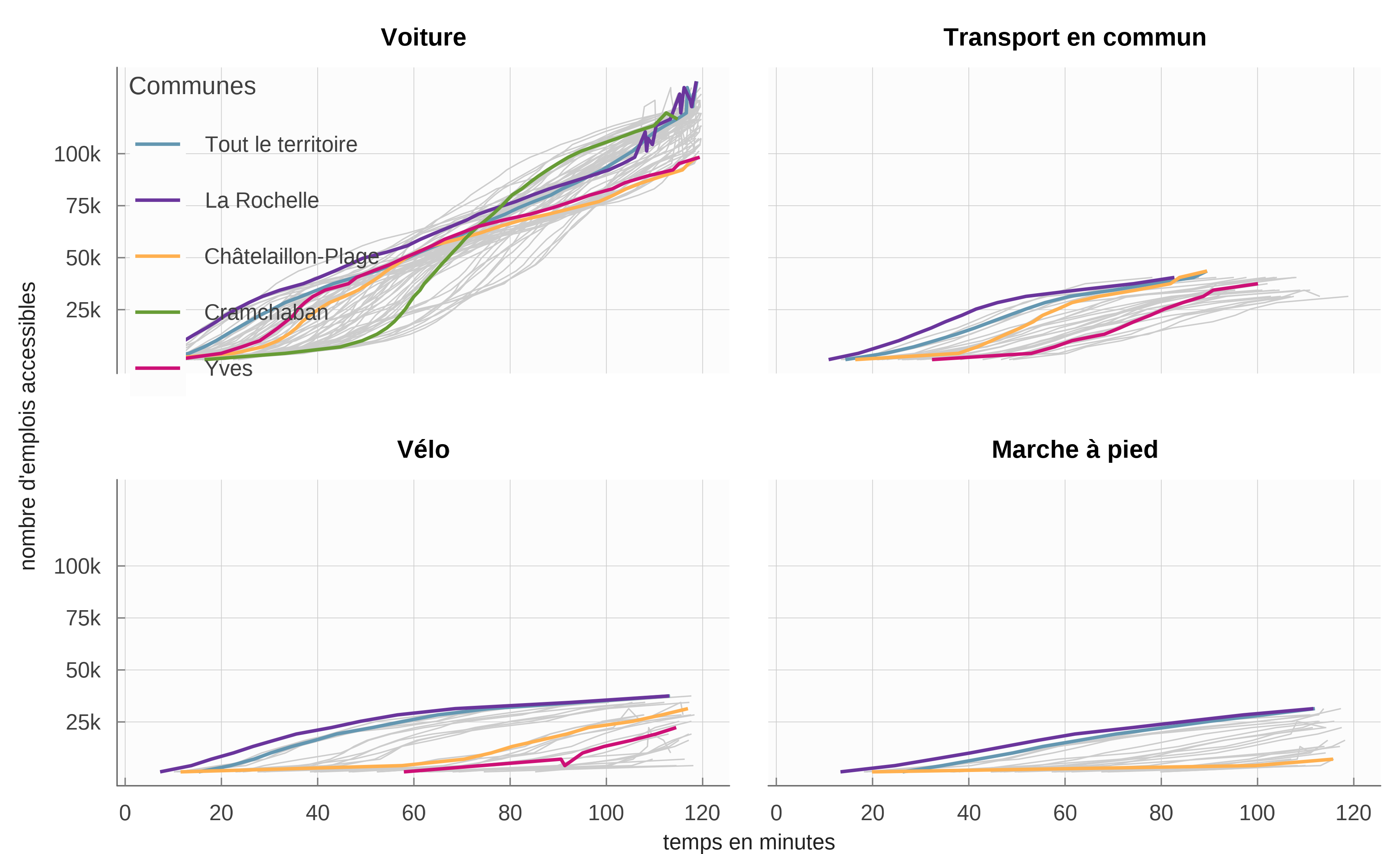
Les courbes d’accessibilité de la figure 6 sont construites en prenant la moyenne par commune de résidence des temps d’accès pour les différents seuils d’emplois. C’est cette courbe qui découle du modèle théorique présenté par ailleurs (Aspects théoriques) et qui détermine les choix individuels de déplacement comme de localisation. Ces courbes font apparaître une propriété propre aux villes littorales : si pour des temps courts, l’accès à l’emploi est maximal à la Rochelle, en revanche d’autres communes jouissent d’une position plus « centrale » lorsqu’on accepte des temps de trajets supérieurs à 30 minutes en voiture.
Sources : OSM, Mapbox, IGN, Conveyal R5, carroyage INSEE 2017, Flores et fichiers fonciers 2018
Encadré 2. Ergodicité
La figure 7 représente le R^2_{KL} que l’on calcule pour le modèle de référence (MEAPS à la maille carreau 200m) en effectuant des simulations de Monte-Carlo pour différentes tailles de l’échantillon d’ordre de priorité. Sans surprise, plus l’échantillon est grand, plus la distribution des R^2_{KL} est étroite. Pour 256 tirages, l’intervalle de confiance à 95% pour le R^2_{KL} est de l’ordre de 0.017% (contre 0.04% pour 64 tirages et 0.003% pour 1024 tirages) ce qui sera suffisant pour la plupart des applications.
La valeur moyenne du R^2_{KL} obtenue pour le MEAPS de référence est de 88.4%.
4.2 Modèle saturé : estimation d’autant d’odds-ratios que de paires de commune
A ce stade, nous utilisons un algorithme naïf pour trouver une solution au problème posé. Nous calculons les odds-ratios \omicron^k_{ij} qui permettraient de combler l’écart entre les prévisions de MEAPS effectuées avec un ensemble d’odds-ratios \omicron^{k-1}_{ij} et les données observées de INSEE (2022a) en utilisant la formule suivante où \beta est un paramètre d’amortissement inférieur à 1 et positif et où k indexe les itérations :
\omicron^k_{ij} = \biggl(\frac{\tilde{c}^k_{abs}}{ c^{mobpro}_{abs}}\biggr)^\beta \times \omicron^{k-1}_{ij} \tag{18}
Nous modifions alors les \omicron_{ij} en fonction des écarts observés. Cela conduit à chercher un point fixe.
L’algorithme naïf est relativement efficace. Il converge en quelques dizaines d’itérations, s’avère stable et fait diminuer l’entropie relative. Il devra être affiné dans le futur afin de permettre une descente de gradient qui permet de minimiser explicitement l’entropie relative. L’algorithme naïf permet de réduire cette entropie relative sans assurer qu’elle est minimale.
Cet algorithme a été utilisé avec différentes contraintes sur les paramètres. Le tableau 7 indique la qualité de l’ajustement obtenu dans ces différentes configurations. La première est celle où les probabilités d’absorption sont déterminées uniquement par les fuites par commune de résidence. C’est la configuration la plus parcimonieuse en termes de paramètres et qui sert de référence. Le R^2_{KL} vaut 88% ce qui est un ajustement élevé. La seconde configuration est celle où l’on ajuste des \omicron_{ij} uniquement pour les termes diagonaux (i=j). Cette configuration ajuste donc un odd-ratio pour les résidents qui travaillent dans leur commune de résidence. Dans un certain nombre de communes, cet ajustement conduit à augmenter la probabilité d’absorption interne (figure 11), ce qui indique que le choix de résidence n’est pas indépendant de celui d’activité. Pour la commune la plus importante (La Rochelle), en revanche, l’odd-ratio \omicron_{17300, 17300} est proche de 1. Les deux configurations suivantes laissent beaucoup plus de degrés de liberté en estimant des \omicron_{ij} librement. La première de ces deux configurations limite les \omicron_{ij} estimés à ceux représentant un total cumulé des flux mesurés par INSEE (2022a) égal à 99.4%, soit 1 854 \omicron_{ij} . La seconde configuration estime tous les \omicron_{ij} sans limite (soit 2 033 paramètres pour 72 communes de résidence et 210 communes d’activité, avec un grand nombre de liaisons non considérées parce que nulles).
| RKL2 | Degrés de liberté | odds estimés | |
|---|---|---|---|
| Référence (odds unitiaires) | 88.4% | 1 752 | 0 |
| Diagonale (résidence égale emploi) | 95.0% | 1 681 | 71 |
| 90% des flux cumulés | 97.4% | 1 027 | 725 |
| 99% des flux cumulés | 99.3% | 0 | 1 849 |
| 100% des flux cumulés | 99.6% | 0 | 2 029 |
| Le nombre de degrés de liberté est le nombre de paires de flux non nuls dans MOBPRO, moins les contraintes en ligne et en colonne, plus un puisqu’elles sont redondantes moins le nombre de paramètres estimés. Le nombre de degré de liberté est nul pour les configurations 99% et 100% arce que le nombre de paramètres estimés est supérieur au produit des linges et des colonnes moins les contraintes. Il y a bien plus de paramètres estimés pour la configuration 100% que pour 99%. En conséquence, l’algorithme conduit à un résultat légèrement différent. | |||
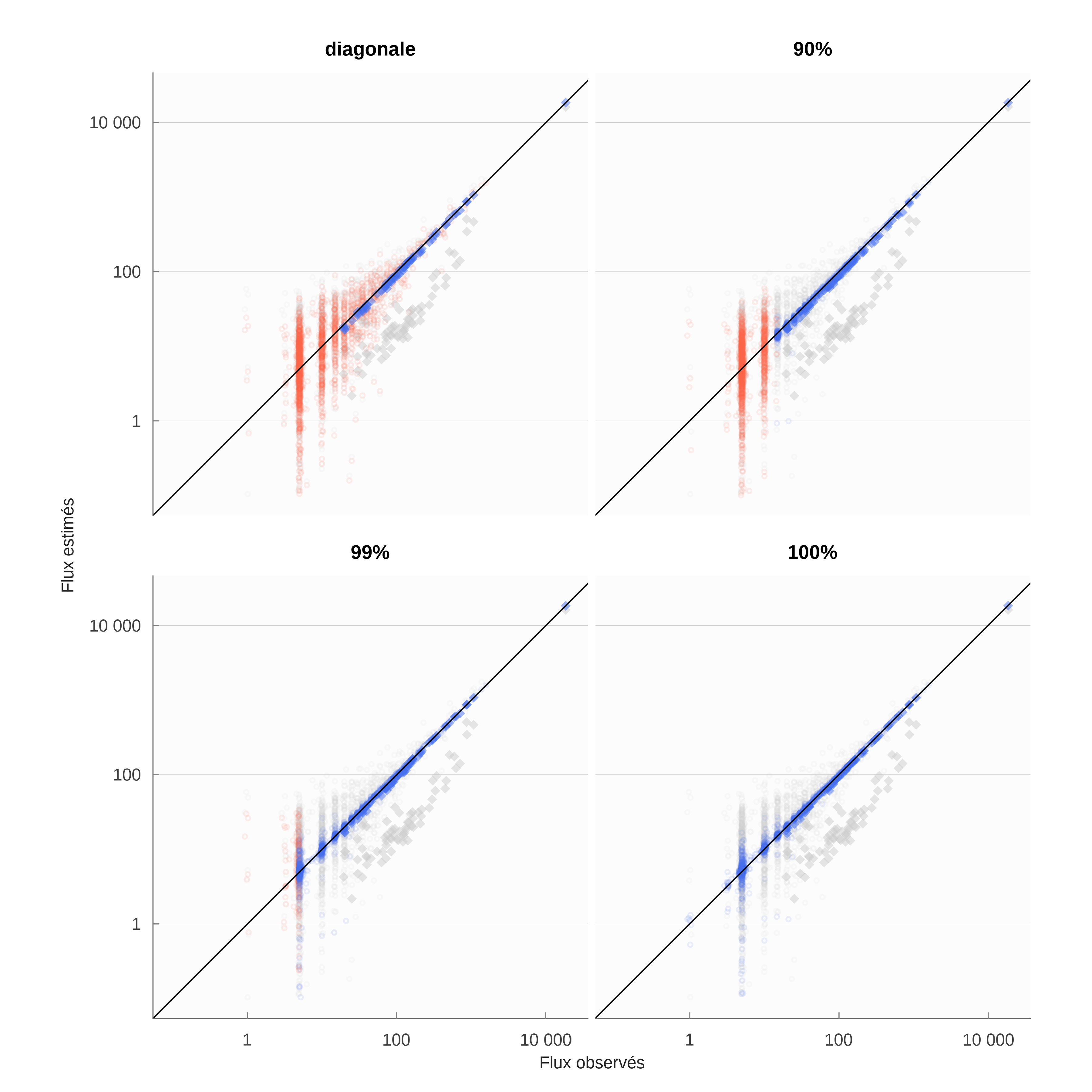
La figure 8 représente les flux observés et estimés pour les différentes configurations du tableau 7. Le fait d’estimer uniquement les \omicron_{ii} diagonaux, en ajustant donc seulement les flux allant d’une commune de résidence vers elle même, donne déjà de très bons résultats en faisant passer le R^2_{KL} de 88% à 95% et en réduisant visiblement les écarts entre flux observé et flux estimé, comme le montrent les deux panneaux supérieurs de la figure 8. L’ajout de paramètres supplémentaires ne fait pas gagner beaucoup plus, d’autant que les écarts pour les flux marginaux ne sont pas tant réduits que ça. La limite de l’algorithme naïf apparaît ici, puisque le modèle complètement saturé n’ajuste pas totalement la distribution. Différents détails de l’algorithme peuvent l’expliquer, notamment la censure des odd-ratio trop faibles (<0.0001) ou trop importants (>10000) ou la prise en compte des flux nuls. Au-delà de cet argument, il est probable que pour converger vers un ajustement plus strict, il serait nécessaire de calculer la matrice des quasi dérivées des flux par rapport aux \omicron_{ij}.
Mais le coût peut être très élevé puisque cette matrice (calculée dans la partie synthétique dans un cas simple) est d’une taille considérable (1 755 \times 1 755 coefficients), surtout si l’on prend en compte que le calcul de chaque terme prend autour d’une vingtaine de secondes9.
9 Autour d’une année de vCPU…
Notons que l’échantillon des mobilités donné par INSEE (2022a) pour l’agglomération de la Rochelle est très particulier. Une commune (La Rochelle, dont le code géographique est 17300) représente presque 29% des flux de mobilité (de La Rochelle lieu de résidence vers La Rochelle lieu d’emploi). C’est donc un schéma monocentrique, où à la fois les résidents et les emplois sont concentrés sur un territoire réduit. La résolution spatiale de INSEE (2022a) ne nous permet pas d’en détailler la structure plus fine.
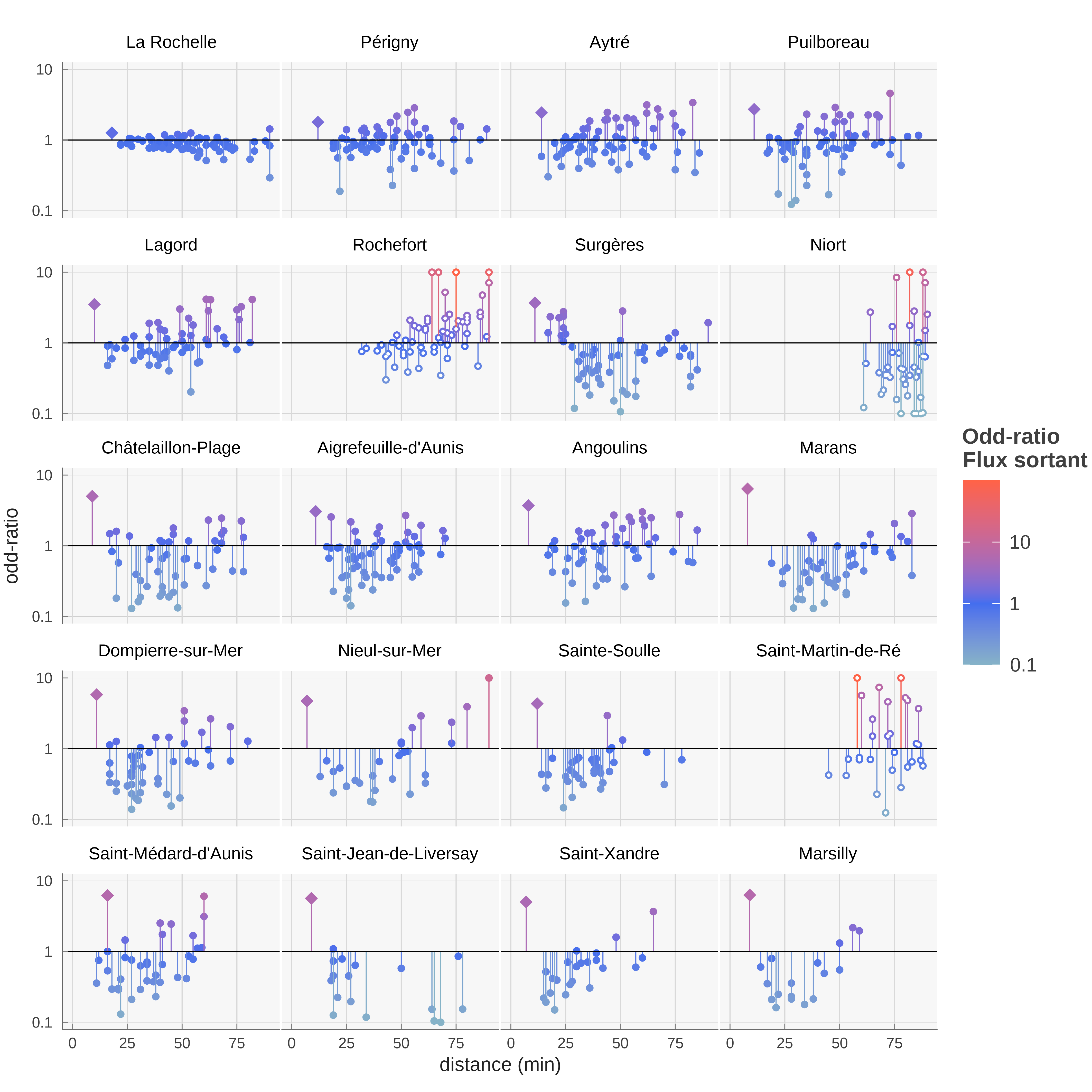
Pour les 20 plus grandes communes de l’agglomération de la Rochelle – qui comptent chacune plus de 1 000 résidents en activité – on peut représenter les odds-ratios estimés dans la configuration 100% des flux par rapport aux chances calculées dans le cas où tous les \omicron_{ij} sont égaux à 1 (des odds-ratios effectifs) en fonction de la distance entre la commune de destination et la commune de résidence10. Ce diagramme, analogue à un spectre, peut aussi être construit par commune de destination, la distance d étant la distance aux différentes communes de résidence (figure 10). L’élément le plus frappant est que les odds-ratios de i à i sont généralement supérieur à 1 (figure 9), à l’exception de la commune de la Rochelle. Il n’émerge pas de structure particulière par rapport à la distance, si ce n’est des odds-ratios élevés pour des distances importantes
10 La distance est construite comme la distance moyenne pondérée entre les résidents de la commune de départ et les emplois de la commune d’arrivée. La pondération est le produit des emplois et des résidents pour chaque paire, normalisé à 1.
La figure 11 permet de préciser la valeur élevée des odds-ratios pour les flux internes. Les communes où sont localisés de nombreux emplois ont un odds-ratio plutôt plus faible alors qu’ils sont estimés plus élevés dans les communes plus petites et moins desservies. Pour les différentes procédure d’estimation et donc différents nombres de paramètres estimés, on observe une structure similaire dans la répartition géographique des odds-ratios, ce qui suggère que les odds-ratios estimés contiennent de l’information.
Un odds-ratio élevé dans la diagonale indique que les flux internes sont plus importants que dans le scénario de référence. Cela indique probablement un choix de résidence en lien avec l’emploi occupé en privilégiant la commune d’activité pour résidence (ou éventuellement l’inverse). Le spectre résident en fonction de la distance indique que ce phénomène, s’il est une hypothèse à très faible distance, ne persiste pas en dehors de la commune de résidence. En revanche, la figure 10 suggère que dans certaines communes, notamment Surgères, on observe des odds-ratios supérieurs à 1 pour des distances faibles, ce qui s’interprète comme le fait que les habitants des communes alentours privilégient Surgères comme lieu d’emploi.
A ce stade, les observations sont limitées par le faible nombre de communes modélisées, mais on peut espérer que l’analyse des odds-ratios estimés pourra servir à caractériser les communes en fonction des choix de résidence et d’emploi. En multipliant cette analyse pour d’autres territoires, l’information apportée par les odds-ratios pourra être inférée. Il sera aussi possible de confronter ces éléments à d’autres variables, comme le prix de l’immobilier, les loyers résidentiels ou commerciaux, la densité d’emploi.
4.3 Estimations paramétriques et comparaison avec le modèle gravitaire
Au lieu d’estimer directement un ensemble d’odds-ratios \omicron_{ij}, on peut proposer des formes fonctionnelles paramétriques à partir desquelles on calculera les odds-ratios. C’est une stratégie bien plus parcimonieuse. On détermine alors les paramètres de la forme fonctionnelle retenue par un algorithme standard de minimisation de l’entropie relative, qui est le critère que nous avons choisi pour comparer les distributions. Il est également possible de conduire une estimation paramétrique pour le modèle gravitaire.
Nous explorons ici trois formes fonctionnelles pour MEAPS :
Un paramètre pour tous les termes diagonaux, c’est-à-dire les flux allant d’une commune de résidence vers cette même commune pour l’emploi. Cette forme est proche de la forme « diagonale » estimé dans la section 4.2, mais un seul paramètre est estimé – par une minimisation de l’entropie relative – au lieu de 72 par l’algorithme itératif. Formellement, \omicron_{i \neq j}=1 et \omicron_{ii} = o.
Un paramètre pour tous les termes diagonaux et un paramètre pour les communes voisines d’emploi, c’est-à-dire un terme correctif reliant une commune de résidence aux communes voisines. Une commune est voisine d’une autre si au moins 5% des trajets pondérés par les emplois et les résidents ont une distance kilométrique inférieure à 3 km. Cette définition permet d’exclure des communes limitrophes mais dont les pôles principaux sont distants. Formellement, \omicron_{ii} = o_d; \omicron_{ij\in \mathcal{V}(i)} = o_v et \omicron_{i, j \neq i, j \notin \mathcal{V}(i)} = 1.
Un coefficient pour la distance et un paramètre pour la distance de « bascule ». Formellement, en dessous d’une distance d_c , on définit un \omicron_{ij \in d_{i,j} \leq d_c} = o et \omicron_{ij \in d_{i,j} > d_c} = 1. Cette forme partage la même idée que le premier modèle, mais estime la notion de proximité au lieu de reposer sur le découpage administratif.
Chacune de ces options mesure un biais intra-communal qui peut s’expliquer par un choix conjoint de localisation de résidence et d’emploi. MEAPS offre ici la possibilité de mesurer l’intensité de ce phénomène par rapport à l’hypothèse où les emplois sont considérés indépendamment de la localisation et sont tous parfaitement substituables. Il sera intéressant de comparer les territoires de ce point de vue et de repérer et quantifier des spécificités locales, qu’elles concernent la géographie du territoire – sa structure en pôles ou en satellite –, la formation des prix de l’immobilier, le réseau de transport ou la nature de l’activité économique. On pourrait également chercher à exploiter l’information sectorielle – disponible dans INSEE (2022a) au niveau de 5 secteurs – ou l’information sociale ou démographique – disponible au niveau communal ou de l’IRIS mais qui peut être exploitée également à un niveau plus fin avec Fidéli11.
11 Fichiers démographiques sur les logements et les individus, INSEE, https://www.insee.fr/fr/metadonnees/source/serie/s1019.
A ces formes fonctionnelles pour MEAPS, nous ajoutons deux formes fonctionnelles pour le modèle gravitaire :
- un modèle gravitaire suivant la définition équation 1 où f(d)= e^{d/\delta}. Un seul paramètre \delta est estimé.
- un modèle gravitaire « équilibré » en utilisant l’algorithme de Furness, tel que décrit plus haut et en estimant \delta comme dans le point 4.
On pourrait multiplier les modèles estimés12. Le propos est ici d’illustrer les possibilités de notre modélisation et de les comparer à celles du modèle gravitaire. Deux points émergent :
12 Par exemple, en faisant dépendre les odd-ratios non pas de la distance et d’une distance critique mais du rang et d’un rang critique.
MEAPS peut mieux reproduire les données, avec une qualité d’ajustement meilleure,
MEAPS ouvre des possibilités d’interprétation plus riches que celle du modèle gravitaire, parce que les fondements microscopiques de MEAPS sont explicites.
Le tableau tableau 8 résume les résultats des estimations. Le modèle de référence, dans lequel tous les emplois sont substituables pour chaque individu, fait moins bien en termes d’ajustement que les autres modèles, à l’exception notable du modèle gravitaire non équilibré. Comme on avait pu le constater dans les estimations non paramétriques, le modèle de référence a, malgré son hypothèse simplificatrice, une bonne performance, ce qui est confirmé ici par la comparaison au modèle gravitaire simple.
| RKL2 | Degrés de liberté | Paramètres | |
|---|---|---|---|
| Référence | 88.4% | 1 752 | |
| 1. Commune vers commune | 93.0% | 1 751 | NA |
| 2. Commune vers commune et voisines | 93.1% | 1 750 | od≈4.3 |
| 3. Distance carreau 200m | 94.1% | 1 750 | dc≈ 9 min |
| 4. Gravitaire sans Furness | 82.6% | 1 961 | δ≈20 min |
| 5. Gravitaire avec Furness | 90.7% | 1 751 | δ≈17 min |
| Le nombre de degrés de liberté est le nombre de paires de flux non nuls dans MOBPRO, moins les contraintes en ligne et en colonne, plus un puisqu’elles sont redondantes moins le nombre de paramètres estimés. Les unités sont des minutes de trajet pour les paramètres homogènes à une distance et sans unité pour les odd-ratios. | |||
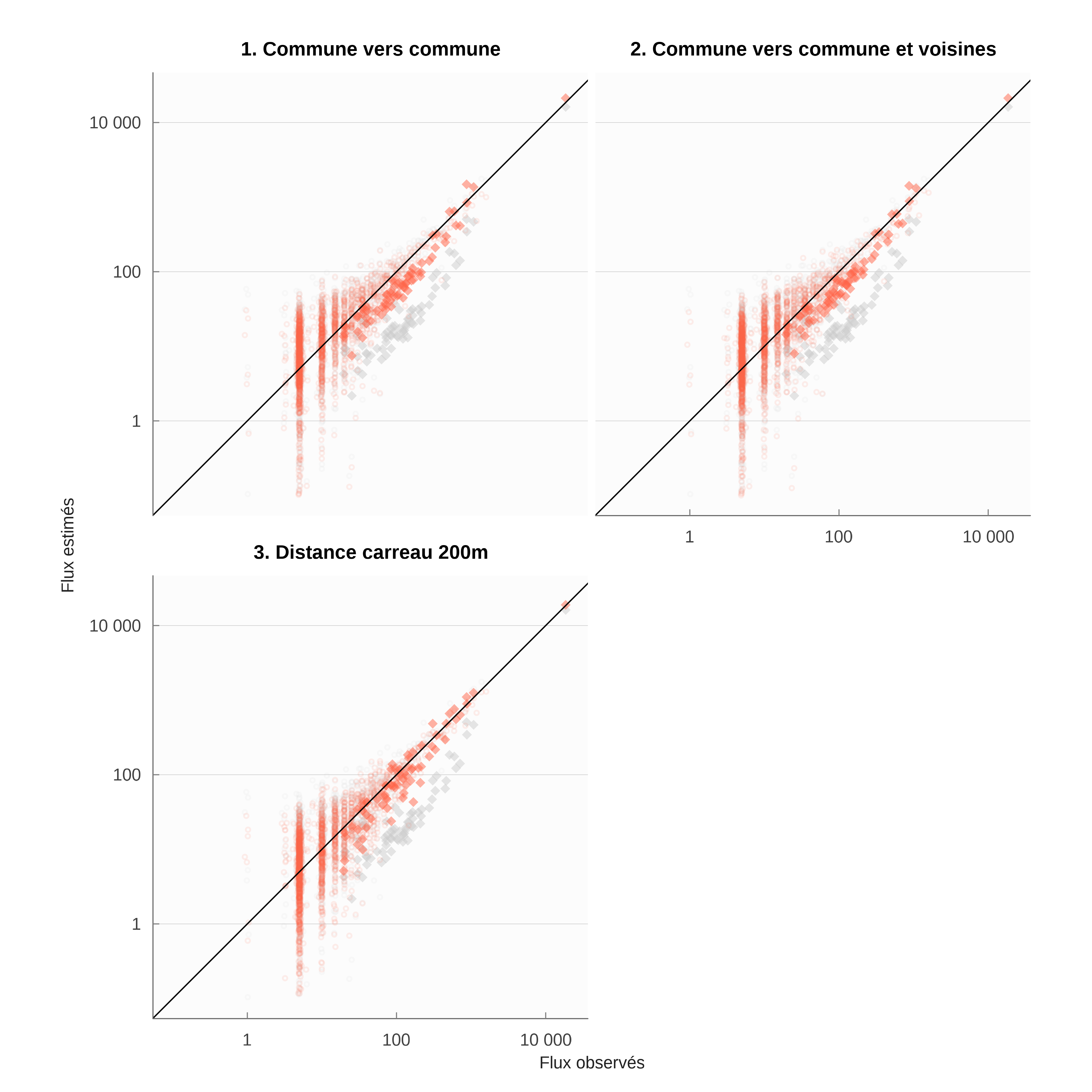
Les estimations des modèles 1 à 3, dans lesquelles on explore un terme diagonal sous différentes formes, renforcent le diagnostic de biais communal noté dans les estimations non paramétriques. Il y a en moyenne 4 fois plus de chance de choisir un emploi (tableau 8, lignes 1 et 2) dans la commune de résidence. L’estimation du modèle 2 montre que les communes voisines ne connaissent pas un biais comparable, bien que la chance de choisir un emploi dans celles-ci soit supérieure à 1.
L’estimation du modèle 3 indique qu’apparemment la distance explique mieux le biais communal que le découpage administratif et il convient plutôt de voir celui-ci comme un biais de proximité. En effet, le coefficient d’ajustement est supérieur de plus d’un point à celui obtenu avec le premier modèle, en perdant uniquement 1 degré de liberté. La distance de bascule est faible, autour de 9 minutes, ce qui suggère que le périmètre communal est trop large pour capturer cet effet. La chance à plus courte distance est également nettement plus élevée puisqu’au lieu d’être approximativement de 4 elle est approximativement de 19, soit plus de 4 fois plus.
Il convient à ce stade d’être prudent sur cette estimation, puisque la résolution des données est largement inférieure au seuil qui a été trouvé. La simulation est basée sur des distances et des localisations d’emplois au carreau 200m dont la précision est convaincante. Mais les flux dans INSEE (2022a) ne sont connus que pour les communes d’origine et de départ et donc avec une résolution spatiale plus faible. La multiplication des observations peut palier à cette faible résolution spatiale, mais cela demandera d’établir une analyse des distances et des localisations sur des territoires plus grands et plus nombreux. Pour avancer, il faudrait recourir à des données de flux plus finement localisées, par exemple à partir de Fidéli13 ou de données issues de traçages numériques.
13 A partir de Fidéli, on peut préciser la localisation de chaque individu et utiliser l’information sur la commune dans laquelle il travaille. On ne peut pas en revanche localiser plus précisément la localisation de l’emploi occupé.
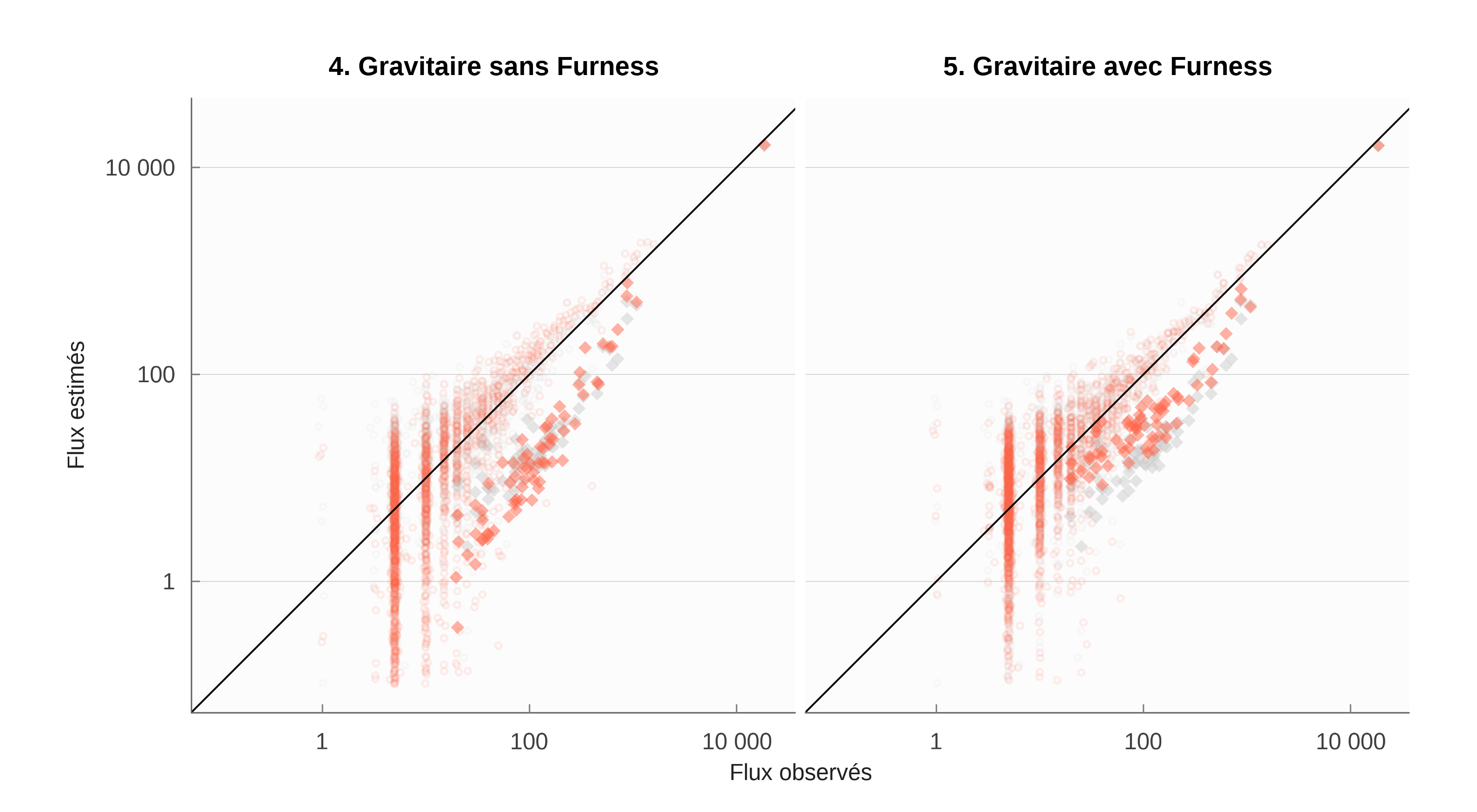
Les estimations paramétriques indiquent une moins bonne performance du modèle gravitaire. Sans respect des contraintes en colonne, le modèle gravitaire donne une image assez faussée des trajets. Il peine à reproduire le biais de proximité et l’influence de la distance. Le premier tend à produire un paramètre \delta très élevé alors que le second devrait au contraire imposer un \delta plus faible pour rendre compte de trajets plus longs. L’application d’une même valeur de la distance suivant des milieux plus ou moins denses handicape cette représentation. La procédure de Furness améliore la capacité du modèle gravitaire à rendre compte des données, mais, comme nous le disions, au prix de la perte du lien avec la distance telle qu’elle est formulée dans le modèle gravitaire, à savoir homogène pour tous.
La figure 13 illustre ce qui est à l’œuvre dans le modèle gravitaire. La minimisation de l’entropie relative dépend beaucoup des flux à l’intérieur de La Rochelle, qui pèsent 29% de l’échantillon. La prise en compte des autres communes diagonales n’est pas bonne, ce qui conduit à un R^2_{KL} moins bons que la référence de MEAPS (tous les emplois sont identiques pour chaque individu et ne diffèrent que par leur localisation). Le respect de la contrainte en colonne par la procédure de Furness permet une meilleure prise en compte des communes diagonales (dont le poids est de 35% dans l’échantillon La Rochelle), mais moins bonne que les modèles MEAPS paramétriques ou non.
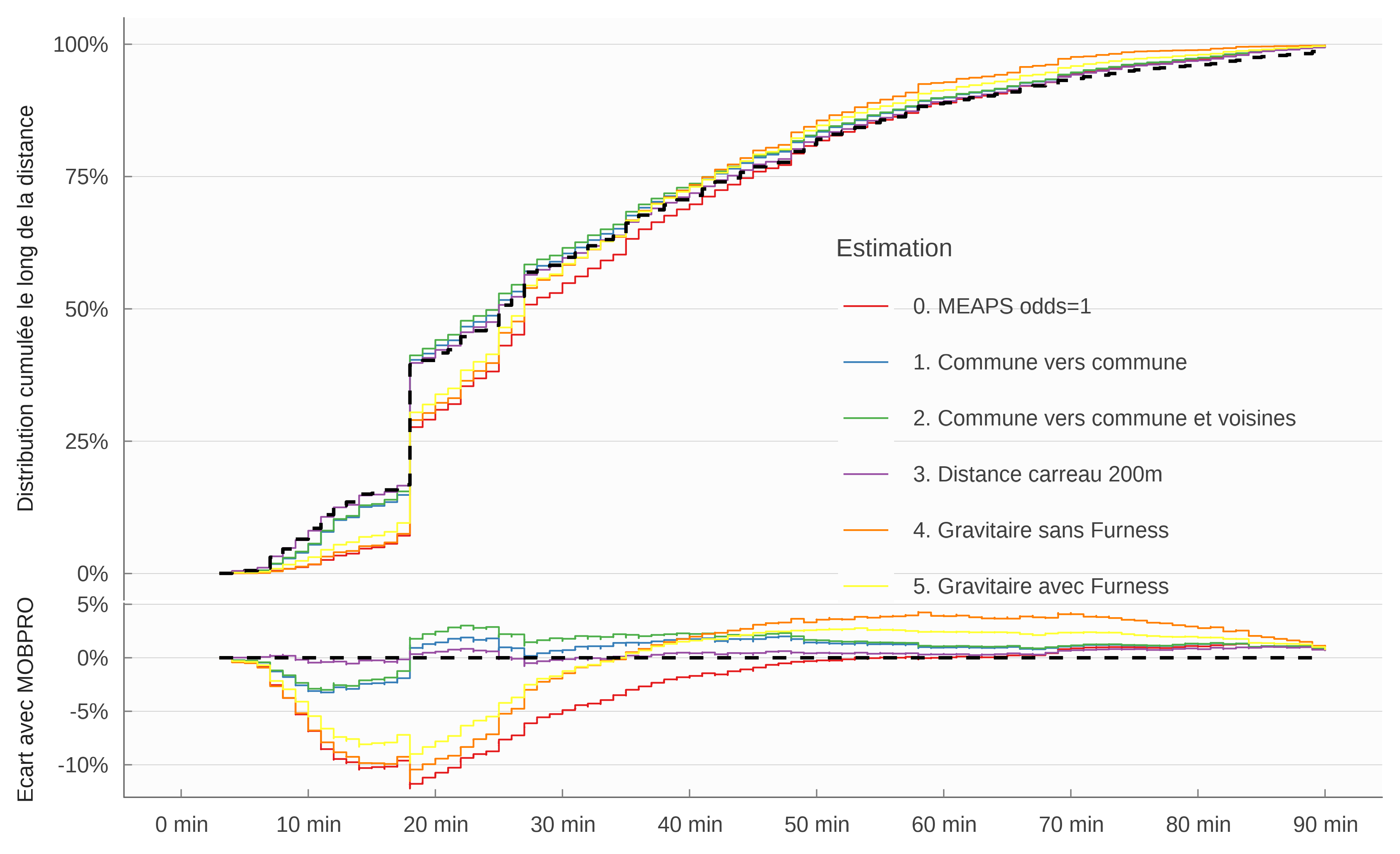
La figure 14 confirme ce diagnostic. On y compare la distrbution cumulée en fonction de la distance kilométrique pondérée entre chaque commune pour différentes estimations, les flux de INSEE (2022a) étant utilisé comme référence. Les performances des modèles sont comparables pour les courtes distances (i.e la commune de la Rochelle vers elle-même). Le modèle gravitaire avec ou sans Furness pêche sur les distances intermédiaires et donne trop de poids aux distances très longues. Les estimations paramétriques à partir de MEAPS parviennent bien à reproduire la distribution cumulée des distances, notamment le modèle paramétrique 3. qui retient la distance au carreau 200m comme forme fonctionnelle.
5 Conclusion
Les estimations que nous présentons ici aboutissent à plusieurs résultats importants :
une métrique pondérée ou d’entropie relative produit des résultats plus robustes, plus convainquant et une capacité de prédiction bien meilleure que la métrique implicite (non pondérée) des moindres carrés ordinaires ;
l’utilisation de données supplémentaires sur la géographie du territoire (localisation des individus, des résidents, réseaux de transport) accroît la qualité des estimation et la capacité prédictive ;
la modélisation des flux par MEAPS a de meilleures propriétés et une plus grande capacité prédictive que le modèle gravitaire, y compris lorsque celui ci est estimé en utilisant une métrique adaptée et une information géographique fine, à partir du moment où l’on introduit des paramètres dans le modèle radiatif. Le modèle radiatif universel et sans paramètre produit un résultat correct, mais l’ajustement est inférieur à ceux de modèles gravitaires paramétrisés ;
les paramètres du modèle gravitaire sont difficilement interprétables. Ils dépendent en effet de la configuration spatiale spécifique et de l’échelle d’observation. MEAPS permet une approche structurelle aux fondements bien définis qui donne aux paramètres une signification plus générale.
Références bibliographiques
Bibliograhie
Agresti A. (2002). « Categorical Data Analysis », Wiley Series in Probability and Statistics.
Aitchison J., Ho C.H. (1989). « The multivariate Poisson-log normal distribution », Biometrika, 76, n° 4, p. 643‑653.
Colin Cameron A., Windmeijer F.A.G. (1997). « An R-squared measure of goodness of fit for some common nonlinear regression models », Journal of Econometrics, 77, n° 2, p. 329‑342.
Conway M.W., Byrd A., Linden M. van der (2017). « Evidence-Based Transit and Land Use Sketch Planning Using Interactive Accessibility Methods on Combined Schedule and Headway-Based Networks », Transportation Research Record: Journal of the Transportation Research Board, 2653, n° 1, p. 45‑53.
Conway M.W., Byrd A., Van Eggermond M. (2018). « Accounting for uncertainty and variation in accessibility metrics for public transport sketch planning », Journal of Transport and Land Use, 11, n° 1.
Conway M.W., Stewart A.F. (2019). « Getting Charlie off the MTA: a multiobjective optimization method to account for cost constraints in public transit accessibility metrics », International Journal of Geographical Information Science, 33, n° 9, p. 1759‑1787.
Dios Ortúzar J. de, Willumsen L.G. (2011). Modelling transport, John wiley & sons.
Flowerdew R., Aitkin M. (1982). « A Method of Fitting the Gravity Model Based on the Poisson Distribution* », Journal of Regional Science, 22, n° 2, p. 191‑202.
Fotheringham A.S. (1983). « A New Set of Spatial-Interaction Models: The Theory of Competing Destinations », Environment and Planning A: Economy and Space, 15, n° 1, p. 15‑36.
Griffith D.A., Fischer M.M. (2016). « Constrained Variants of the Gravity Model and Spatial Dependence: Model Specification and Estimation Issues », dans Patuelli R., Arbia G. (dirs.), Springer International Publishing, Cham, p. 37‑66.
INSEE (2022b). « Revenus, pauvreté et niveau de vie en 2017 - Données carroyées. Dispositif Fichier localisé social et fiscal (Filosofi) »,.
INSEE (2022a). « Mobilités professionnelles en 2019 : déplacements domicile - lieu de travail Recensement de la population - Base flux de mobilité »,.
Josselin D., Carpentier-Postel S., Audard F., Amarouch S., Durand J.-B., Brachet N., Coulon M., Garcin L. (2020). « Estimer des flux de navetteurs avec un modèle gravitaire : application géomatique en région Provence-Alpes-Côte d’Azur (France)1 », Geomatica, 74, n° 3, p. 104‑130.
Kullback S., Leibler R.A. (1951). « On Information and Sufficiency », The Annals of Mathematical Statistics, 22, n° 1, p. 79‑86.
Lenormand M., Bassolas A., Ramasco J.J. (2016). « Systematic comparison of trip distribution laws and models », Journal of Transport Geography, 51, p. 158‑169.
Masucci A.P., Serras J., Johansson A., Batty M. (2013). « Gravity versus radiation models: On the importance of scale and heterogeneity in commuting flows », Physical Review E, 88, n° 2, p. 022812.
Pereira R.H.M., Marcus Saraiva, Daniel Herszenhut, Carlos Kaue Vieira Braga, Matthew Wigginton Conway (2021). « r5r: Rapid Realistic Routing on Multimodal Transport Networks with R5 in R »,.
SDES (2021). « EMP 2019 Résultats détaillés de l’enquête mobilité des personnes de 2019 »,.
Sen A., Smith T.E. (1995). Gravity Models of Spatial Interaction Behavior, Springer, Berlin, Heidelberg (Advances in Spatial et Network Economics).
Réutilisation
Citation
BibTeX
@article{parodi2024,
author = {Parodi, Maxime and Timbeau, Xavier},
title = {MEAPS \& gravitaire : estimations à La Rochelle},
journal = {Document de travail de l’OFCE n°2024-4},
date = {2024-02-02},
url = {https://preview.meaps.fr},
langid = {fr},
abstract = {L’estimation de modèles gravitaires est faite usuellement
en utilisant les moindres carrés ordinaires. Nous montrons que la
distribution des flux de navetteurs correspond mal à un modèle où
l’erreur est log-normale. La représentation par une processus de
Poisson, que l’on peut estimer par glm est plus apropriée. A partir
de la log-vraisemblance, on remarque que l’estimation par glm est
équivalente à la minimisation de l’entropie relative de
Kullback-Leibler, ce qui permet l’estimation par minimisaiton non
linéaire d’une famille plus grande de modèles, dont MEAPS. La
discussion des effets fixes ou aléatoires permet de comprendre en
quoi la modélisation respecte ou non les contraintes aux marges du
problème. On montre que les modèles qui respectent ces marges
peuvent être employés hors échantillon pour prédire les flux de
navetteurs. enfin, en utilisant une information infracommunale on
peut améliorer la qualité de l’ajustement de MEAPS et produire une
intrapolation des flux à une résolution plus importante que celle
des données de flux issues du recensement. \textless
br\textgreater{} `r wordcountaddin::word\_count(“larochelle.qmd”)`
mots.}
}
Veuillez citer ce travail comme suit :
Parodi M., Timbeau X. (2024). « MEAPS & gravitaire : estimations à
La Rochelle », Document de travail de l’OFCE
n°2024-4.