| e1 | e2 | e3 | |
|---|---|---|---|
| h1 | 0.00 | 0.75 | 0.75 |
| h2 | 0.75 | 0.00 | 1.50 |
| h3 | 0.75 | 1.50 | 0.00 |
MEAPS : Modéliser les flux des navetteurs
Le modèle gravitaire utilisé pour distribuer les trajets entre une origine et une destination représente mal l’influence de la distance sur les choix. En s’inspirant du modèle des ‹intervening opportunities› de Stouffer (1940) et du modèle radiatif de Simini et al. (2012), nous construisons un modèle ergodique d’absorption avec priorité et saturation (MEAPS) qui permet de construire ces choix sur des fondements microscopiques clairs et flexibles. Le modèle s’accommode de différentes formulations des processus stochastiques qui permettent d’estimer des paramètres fondamentaux et de leur donner une interprétation. Nous validons le modèle théorique sur des données synthétiques, puis dans deux documents associés (Parodi et Timbeau, 2024b, 2024a), nous proposons une estimation de MEAPS et une comparaison détaillée avec le modèle gravitaire et ses variantes les plus communes. Nous utilisons ensuite cette modélisation pour construire une carte en haute résolution des émissions de CO2 à La Rochelle.
5797 mots.
5797 mots.
1 Tobler n’implique pas la gravité
Dans l’analyse des phénomènes spatiaux, la distance joue un rôle important. Cette évidence est ce qu’on appelle parfois le principe de Tobler :
Tout est relié mais les choses proches sont plus reliées que les choses éloignées.
Si nous prenons l’exemple de l’appariement géographique des emplois et des résidents, la proximité de l’emploi est un facteur incontournable, même si d’autres facteurs interviennent dans le choix d’un emploi : le salaire, les compétences, etc. Le rôle de la distance lors du choix d’un emploi est évalué généralement à l’aide d’un modèle gravitaire. Peu d’alternatives ont été étudiées dans la littérature et le modèle gravitaire s’est imposé comme un standard, un outil que l’on peut oublier pour se consacrer à la prise en compte des autres facteurs.
Pourtant, en nous intéressant à la mobilité de la vie quotidienne à une échelle géographique fine – le carreau 200 mètres – nous nous sommes heurtés aux limites du modèle gravitaire, en particulier lorsqu’il a fallu se prononcer sur des scénarios de relocalisation de l’emploi. Ces limites tiennent à ce que le modèle gravitaire réduit le principe de Tobler à une mesure homogène de la distance. Il est possible d’améliorer nettement la compréhension des territoires en passant de la distance aux temps de transport selon les différents modes possibles. Plus finement encore, il est possible de passer à une notion de coût généralisé d’un déplacement, qui prend en compte différents aspects de ce trajet (son coût monétaire, son confort, sa fiabilité, etc.). Toutefois, ces améliorations de la « métrique » – certes indiscutables – ne font que changer l’input du modèle gravitaire, sans l’interroger. Or ce modèle souffre d’un défaut plus fondamental : il évacue ce qui fait la spécificité du spatial en voulant réduire celui-ci à une variable unidimensionnelle ; il évacue le fait que l’espace est habité et que chaque lieu est défini aussi par son voisinage.
Ainsi, le modèle gravitaire traite de la même façon les milieux urbains denses et les zones rurales. Il faudrait croire, par exemple, qu’un trajet d’une demi-heure en voiture est aussi pénible pour un gilet jaune que pour un Parisien. Or ce n’est évidemment pas le cas : celui qui réside en milieu rural fait de nécessité vertu et finit même par apprécier ces longs trajets quotidiens, tandis que celui qui réside dans des zones fortement urbanisées envisage des alternatives puisqu’il dispose d’un plus large éventail de possibles pour satisfaire ses demandes. Le défaut du modèle gravitaire n’est pas ici une simple histoire de relation subjective au temps de trajets. Plus fondamentalement, le défaut tient à ce que ce modèle ne voit pas l’espace ; il ne voit pas ce que le territoire offre ; il ne voit pas qu’en zone urbaine l’offre (d’emplois, de services, …) est plus ramassée et que cela change la manière de traiter les distances relatives et les coûts relatifs. La conséquence de cet aveuglement est que l’offre sur le territoire est traité comme si elle était homogène. Supposons, par exemple, que les pouvoirs publics souhaitent créer une zone industrielle offrant de nouveaux emplois. Le modèle gravitaire conduira à penser que les résidents en zone rurale, parce qu’ils sont très parsemés, sont le plus souvent trop éloignés de la nouvelle zone d’emplois pour être intéressés : dans l’arbitrage entre utilité de l’emploi et coût du trajet, ce dernier devient rapidement si élevé qu’il semble préférable de renoncer à l’emploi. Or, l’arbitrage réel est loin d’être aussi simpliste car, bien entendu, un individu qui ne trouve pas d’emplois à proximité se résignera à faire plus de kilomètres pour travailler que quelqu’un qui, au contraire, vit près d’un centre économique dynamique. La distance ne pèse pas du même poids selon la quantité d’offre dans le voisinage.
Face à ces anomalies liées au modèle gravitaire, nous proposons de nous appuyer sur une autre analogie : celle de la traversée par un flux de particules d’un matériau composé de sites d’absorption hétérogènes. Si l’on cherche un emploi dans une zone riche en emplois, la chance d’être satisfait à proximité de son point de départ sera importante, comme l’est la chance d’une particule d’être rapidement absorbée lorsqu’elle est entourée de sites absorbants. A l’inverse, si les emplois sont peu denses là où on réside, la distance à parcourir sera probablement plus grande, comme une particule traversant une zone de vide. En fait, la chance d’être absorbée ne dépend pas directement de la distance au site réceptacle ; elle dépend du nombre de sites qui sont traversées avant celui-ci. Ou, disons encore, elle dépend du rang de ce site dans le classement des sites du plus proche au plus éloigné. Cette analogie se trouve déjà chez Stouffer (1940) et Simini et al. (2012). Toutefois, les modèles qu’ils ont développés peuvent encore être améliorés, notamment en modélisant le fait que les sites d’absorption peuvent avoir une capacité limitée. Le voisinage joue alors à la fois par les emplois, plus ou moins denses autour de moi, mais aussi par les concurrents pour cette ressources, eux même plus ou moins denses autour de moi.
Nous proposons donc un modèle qui tient compte de l’absorption et de la saturation. Il est de nature stochastique et, par un raisonnement de physique statistique, nous pouvons conjecturer une stationnarité des principales prédictions. Nous l’avons appelé Modèle Ergodique à Absorption et Saturation, qui s’abrège en MEAPS.
Ce modèle respecte tout autant le principe que ce qui est proche joue – toutes choses égales par ailleurs – un rôle plus important que ce qui est loin. Mais au lieu de la distance, on utilise le rang dans le classement des distances. La différence peut sembler mineure, mais elle répond à la question de l’hétérogénéité spatiale et de la densité des milieux traversés. Dans le modèle gravitaire, il arrive toujours un moment où, pour prendre encore un autre exemple, l’école est trop éloigné et où ça ne « vaut » plus le coût. Dans la perspective initiée par Stouffer, et reprise ici, l’école la plus proche, celle de rang 1, aussi éloignée soit-elle, demeure utile précisément parce qu’elle est la plus proche. La remarquable série de documentaires intitulée « Les chemins de l’école » souligne parfaitement que l’école la plus proche vaut toujours le coup, même si les écoliers doivent marcher plusieurs heures pour y aller.
L’analogie employée permet de considérer le processus d’appariement comme résultant d’une procédure de recherche qui examinerait les opportunités dans l’ordre de leur proximité. Une telle procédure permet de spécifier des comportements qui servent de référence et d’hypothèse nulle pour se confronter aux données. Des amendements à la marge de cette procédure de recherche pourront produire un meilleur ajustement et s’interpréter directement. Pour l’heure, nous oublions ici tous les autres déterminants de l’appariement, comme le salaire, les compétences demandées ou offertes ou encore le secteur d’activités. Nous ajustons un modèle réduit à l’argument de la distance sur des données riches, issues du recensement français et mesurant les flux entre communes de résidence et communes d’emplois. Sous l’hypothèse que tous les emplois ne diffèrent que par leur localisation, nous parvenons à un ajustement de données bien meilleur que le modèle gravitaire. Des données plus fines – à supposer qu’elles existent – pourraient améliorer encore l’ajustement en introduisant par exemple les différences de salaires ou de compétences. Cependant, une prise en compte plus rigoureuse de la géographie nous semble une première étape essentielle, puisqu’elle modifie d’un ordre de grandeur au moins la qualité de l’ajustement.
L’approche est donc structurelle : c’est un modèle, même frustre, qui définit la façon dont on peut interpréter les données. Les données sans le modèles ne veulent pas dire grand chose, le modèle sans les données n’est que spéculation, et, suivant l’injonction de Kant, nous associons l’un avec les autres pour décrire la réalité.
Ce document décrit la construction du modèle théorique. Nous y développons la critique du modèle gravitaire (section 2), filons l’analogie du modèle radiatif (section 3). Le modèle complet n’est pas solvable dans une forme fermée. Nous décrivons donc un algorithme qui permet de le simuler. Dans une seconde partie (section 4) nous analysons les principales propriétés du modèle théorique sur des simulations synthétiques, c’est-à-dire générés à partir de processus connus. Ceci permet en particulier de donner de la vraisemblance, à défaut d’une démonstration, à la propriété d’ergodicité du modèle, qui conditionne la possibilité de le simuler.
Dans deux autres documents, nous procédons à l’estimation du modèle sur des données réelles et à une comparaison détaillée avec le modèle gravitaire et ses variantes les plus communes (Estimations à La Rochelle). Nous utilisons ensuite cette modélisation pour discuter du lien entre densité et émissions de CO2 (Ville compacte). Nous construisons une carte en haute résolution des émissions de CO2 à La Rochelle à partir d’une projection qui intègre les comportements de fréquence et d’association de motifs pour différentes catégories de ménages.
2 Modélisation gravitaire
Pour modéliser les trajets entre des lieux de résidence et des lieux d’emploi, on procède usuellement par la méthode à 4 étapes (Dios Ortúzar et Willumsen, 2011 ; Patrick Bonnel, 2001). Cette méthode consiste dans un premier temps à déterminer d’un côté le nombre de trajets en partance d’un lieu de résidence et, d’un autre côté, le nombre de trajets arrivant au total dans un lieu d’activité. C’est l’étape 1 de génération des trajets. La seconde étape consiste à distribuer les trajets de l’étape 1 entre chaque paire origine-destination. C’est l’étape de distribution. La troisième étape est celle du choix modal où un mode de transport adéquat est associé à chaque trajet. Enfin la quatrième étape du modèle est celle qui spécifie le trajet et permet d’en connaître les caractéristiques précises, comme le chemin emprunté ou les dénivelés effectués, pour en déduire notamment des prévisions de congestion. Cette décomposition est quelque peu arbitraire et ne rend pas justice de l’état de l’art sur les bonnes pratiques pour articuler ces 4 moments. Par exemple, le nombre de trajets effectué dépend des possibilités ouvertes par la géographie, qui sont définies par les caractéristiques précises des trajets. L’étape 4 est donc nécessaire pour comprendre l’étape 1, et l’étape 4 demande de connaître les choix modaux pour être utile aux choix fait en 1. L’étape 2 est nécessaire pour explorer les possibilités de trajets. Les imbrications sont nombreuses entre les étapes et la décomposition n’interdit pas d’effectuer des allers et retours entre les diverses étapes.
Le modèle que nous développons porte sur l’étape 2, celui de la distribution des trajets entre les différentes paires origines-destinations, ou encore résidences-emplois . Le modèle gravitaire est largement dominant dans cette deuxième étape pour prendre en compte le rôle de la distance dans l’arbitrage entre différentes destinations.
Nous discutons dans une première partie des insuffisances du modèle gravitaire section 2.1. Puis nous présentons le modèle des opportunités intervenantes de Stouffer (1940) et le modèle radiatif de Simini et al. (2012) et Simini, Maritan et Néda (2013). Ils font tout deux intervenir le rang de classement des emplois plutôt que la distance section 2.2 en s’appuyant sur une analogie plus adéquate aux échelles géographiques que nous considérons (commune, région) que celle de la gravitation. Enfin, dans la continuité de ces approches, nous développons un modèle qui repose sur les deux idées suivantes :
Les individus font leurs arbitrages non pas en fonction directement de la distance, mais en fonction du rang (dans l’ordre des distances) des opportunités qui se présentent à eux. Une autre façon de le voir est que le nombre d’emplois accessibles dans un cercle de rayon donné est une meilleure métrique que la distance.
Chaque destination a une capacité d’accueil limitée et il faut donc introduire une notion de saturation qui oblique les individus a aller voir ailleurs. De cette manière, nous donnons un fondement microscopique au respect des contraintes aux marges (tout individu a un emploi, tout emploi est occupé par un individu) et introduisons le voisinage à la fois à la destination mais aussi à l’origine.
La formulation finale est probabiliste et nous en analysons quelques propriétés par des simulations synthétiques (section 4), en montrant que l’on peut arriver rapidement à simuler un état indépendant des conditions initiales.
2.1 Les insuffisances du modèle gravitaire
Le modèle gravitaire développe une analogie avec le modèle de la gravitation universelle d’Isaac Newton dont les succès en physique et en mécanique sont indiscutables. Ce modèle s’impose comme la pierre angulaire de l’étape de distribution des trajets (Dios Ortúzar et Willumsen, 2011 ; Patrick Bonnel, 2001, p. 160 ; Sen et Smith, 1995). Il est également utilisé dans d’autres domaines, comme le commerce international ou l’analyse des épidémies, domaines que nous ne discuterons pas ici.
Les (mauvaises) raisons du succès du modèle gravitaire
Formellement, le modèle gravitaire décrit la force d’une relation entre deux objets en fonction de leur distance et de leur masse respective. Par analogie, le modèle gravitaire consiste ici à évaluer le nombre de trajets professionnels entre deux localisations en prenant pour masses le nombre d’habitants au point de départ et le nombre d’emplois au point d’arrivée et, au dénominateur, une fonction f croissante de la distance1. On a ainsi, en indiçant les points de départ par i et les points d’arrivée par j :
1 La distance peut être n’importe quelle métrique qui distingue les points de l’espace. On pense canoniquement à la distance euclidienne, mais le modèle s’accomode de distances par les réseaux de transport, de temps de parcours pour prendre en compte des vitesses différentes par mode, par type de voies empruntées, par heure de déplacement ou encore pour comparer des modes pour lesquels la distance n’a que peu de signification (transport en commun, du fait du temps d’attente et des voies spécifiques). On peut également envisager un coût complet (intégrant à la fois le coût en temps mais aussi monétaire du mode de transport) ou encore un coût généralisé incluant le confort ou la sécurité perçue et associés au mode de transport. On peut en suivant Koenig (1980), utiliser le logsum pour prendre en compte la variété des solutions pour se rendre à sa destination.
T_{i,j} = \frac {N_{hab, i}\times N_{emp, j}} {f(d_{i,j})} \tag{1}
Les premiers modèles gravitaires ont emprunté la fonction f à la physique newtonienne (f=d^2), mais d’autres formulations ont depuis été proposées. Par exemple, la fonction f=e^{d/\delta} intervient dans les modèles de choix discrets proposés par McFadden (Ben-Akiva et Lerman, 2018 ; McFadden, 1974). En remplaçant la distance par la notion de coût généralisé du transport, on peut relier cette forme fonctionnelle à un modèle de choix avec une fonction d’utilité aléatoire (random utility model). Il est également possible d’ajuster des formes fonctionnelles plus complexes en ajoutant des paramètres. Le modèle gravitaire arrive alors à reproduire plus ou moins des distributions de distances observées dans des enquêtes de mobilité.
Un raisonnement par minimisation de l’entropie a été proposé par Wilson (1967) pour donner un fondement théorique à l’équation 1. Il considère l’état de référence comme étant celui qui est le plus fréquent dans une distribution aléatoire des choix. Wilson (1967) montre alors que, si la fonction f est donnée, l’équation 1 a bien la forme proposée et que c’est le produit des habitants et des emplois qui doit se trouver au numérateur (et non une puissance de l’un ou l’autre par exemple). Mais rien ne permet de trouver un fondement à la forme fonctionnelle de f. Le parallèle avec la physique est simple à faire : l’interaction définit le rôle de la distance, la maximisation de l’entropie permet d’en déduire que l’équation macroscopique dépend des masses agrégées, mais ne permet de dire quoique ce soit de plus sur la nature de l’interaction.
Comme le notent Simini et al. (2012), les fondations théoriques et empiriques de la fonction f sont au mieux faibles. La multiplication des paramètres pour améliorer l’ajustement n’ont le plus souvent aucune justification théorique. De fait, on perd souvent toute possibilité de donner une signification aux paramètres estimés ce qui rend l’exercice d’ajustement opaque. Les comportements asymptotiques soulignent également des incohérences : par exemple, en faisant tendre vers l’infini les emplois à l’arrivée, le modèle prédit un nombre infini de trajets, même si le nombre de résidents au départ est limité ! Il est également insatisfaisant que le modèle gravitaire soit déterministe et ne permette ni d’expliquer les fluctuations statistiques du nombre de trajets prédits, ni d’évaluer la vraisemblance de différents cas empiriques.
Mais la critique la plus forte du modèle gravitaire vient de ses propriétés fondamentales et des conclusions que l’on peut en tirer. Le nombre de trajets entre une origine (la résidence) et une destination (l’emploi) repose sur un simple arbitrage entre distance et quantité de résidents ou d’emplois. Le comportement du modèle aux limites, à nouveau, suscite la perplexité : un seul emploi à l’origine devrait être infiniment préféré un très grand nombre d’emplois un peu plus loin. C’est tout à fait irréaliste et l’on devine déjà que la distance ne joue pas un rôle si direct dans les comportements de mobilité. On voit également que le poids relatif de cet emploi quasi central par rapport aux « masses » d’emplois éloignés va varier de manière irréaliste selon qu’il est plus ou moins proche de l’origine.
Comme le soulignait déjà Stouffer (1940), ce n’est peut-être pas tant la distance aux emplois qui est décisive que le rang de ces emplois selon l’ordre des distances. Dans le modèle gravitaire, il faut faire une grande différence entre le cas où le deuxième emploi le plus proche est à 500 m et le cas où il est à 1 km. Si l’on applique le modèle newtonien, il faudrait croire, par exemple, que l’attractivité de ce dernier emploi est divisée par 4. Qui peut croire que 500 m de différence pèsent d’un si grand poids dans une recherche d’emploi ? L’attractivité de l’emploi dépend avant tout du fait qu’il s’agit du deuxième emploi disponible près de chez soi. Empiriquement, il y a peu de doutes que le modèle gravitaire a de piètres performances : il ne parvient pas à expliquer pourquoi, lorsque la densité des emplois est faible autour d’un résident, celui-ci va envisager des trajets plus long pour atteindre des zones denses en emplois ; c’est pourtant une observation très commune qui devrait se retrouver dans une modélisation adéquate.
Simini et al. (2012) donnent quelques exemples pour les Etats-Unis de la difficulté du modèle gravitaire à reproduire les comportements observés en en stylisant quelques régularités. A l’évidence, le modèle gravitaire ne prédit que des destinations proches et néglige complètement les destinations lointaines. Il semble impossible à la forme fonctionnelle f(d_{ij}) de rendre compte empiriquement à la fois du nombre de trajets courts et du nombre de trajets distants au travers d’un modèle susceptible de rendre compte des trajets dans différentes régions, dès lors que les densités y sont distribuées différemment.
Assez peu de publications se risquent à une comparaison systématique du modèle gravitaire avec d’autres formulations qui respecteraient la première loi de Tobler. On peut citer Heanue et Pyers (1966) comme une des premières tentatives de ce genre. Des travaux récents de (Commenges, 2016 ; Floch et Sillard, 2019 ; Lenormand, Bassolas et Ramasco, 2016) confirment ce que Masucci et al. (2013) concluaient après la publication initiale du modèle radiatif : le modèle gravitaire étendu aurait un meilleur pouvoir explicatif en ce qui concerne les flux de mobilités inter communaux, cette constante tenant pour de nombreuses zones considérés dans plusieurs pays. L’extension habituelle du modèle gravitaire consiste à écrire, où c, \alpha, \beta et \delta sont des paramètres positifs :
T_{i,j} = c \frac {N_{hab, i}^\alpha \times N_{emp, j}^\beta} {d_{i,j}^\delta} \tag{2}
Les paramètres estimés \alpha et \beta sont habituellement inférieurs à 1, ce qui rejoint un problème soulevé par Simini, Maritan et Néda (2013) : dans cette forme le modèle gravitaire est non séparable. Si l’on considère une zone dans laquelle se trouvent des actifs (origine) ou des emplois (destination) et que l’on décide de la séparer en deux zones distinctes 1 et 2 aussi proches que possible , les flux T_1 et T_2 prévus par la forme estimée de équation 2 ne sont pas la somme du flux que l’on obtiendrait des deux zones réunies. La raison de la séparation est que l’on modifie l’unité spatiale d’agrégation (Modifeable Areal Unit Problem) ou que l’on distingue des sous populations (par exemple par secteur, par catégorie de ménage) au sein de la zone initiale. Cette plus grande finesse de description peut se faire avec des comportements de flux différents (ce qui justifie la distinction), mais dans le cas limite où ces populations ne sont pas distinguables, il n’y a pas de raison d’en attendre des comportements différents.
La propriété de séparabilité à l’origine comme à la destination est vérifiée pour le modèle radiatif. Comme Simini, Maritan et Néda (2013) le suggèrent, les paramètres \alpha et \beta du modèle gravitaire peuvent s’expliquer à travers le modèle radiatif (voir plus bas). Ils résument l’information spatiale supplémentaire, et dépendent de la distribution spatiale jointe des masses aux origines et aux destinations. Mais ces deux paramètres sont alors très dépendants à la fois de cette structure spatiale, du découpage unitaire effectué ou de sous-périmètres considérés. En ce sens, on retrouve l’analyse de Fotheringham (1983) selon laquelle il manque au modèle gravitaire une information spatiale essentielle à propos des voisinages.
Le voile de la contrainte aux marges
Le modèle gravitaire peut être encore complexifié pour mieux coller aux données qu’il ne le fait spontanément. Il perd alors un lien clair avec les réflexions théoriques le reliant à la maximisation de l’entropie (Wilson, 1967) ou au modèle de choix discret. L’ajustement du modèle devient un exercice factice dans lequel il est difficile d’avoir confiance en particulier dans l’analyse des scénarios modélisés. L’exercice consiste à ajouter une étape de « normalisation » en incorporant des coefficients correctifs en ligne et en colonne dans la matrice origine-destination, ce qui revient à ajouter des effets fixes à chacun des points de départ et d’arrivée. La formulation du modèle gravitaire est alors modifiée comme suit :
T_{i,j} = a_i \times b_j \times \frac {N_{hab, i}^\alpha \times N_{emp, j}^\beta} {f(d_{i,j})} \tag{3}
La détermination des coefficients a_i et b_j pose de nombreux problèmes. Ces coefficients doivent permettre de respecter les contraintes aux marges : la somme des emplois pour une ligne de résidents doit être égale au nombre des résidents employés dans la zone et la somme des résidents employés sur un lieu d’emploi doit, en colonne donc, être égale au nombre d’emplois en ce lieu. On a pour a_i (en remarquant que \Sigma_j T_{ij} = N_{hab,i} et que \Sigma_i T_{ij} = N_{emp,j} :
\begin{aligned} a_i &{}= \frac {\Sigma_j T_{i,j}} {\Sigma_j \frac {b_j \times N_{hab, i}^\alpha \times N_{emp, j}^\beta}{f(d_{i,j})}} \\ &{}= \frac{N_{hab}^{1-\alpha}} {\Sigma_j \frac{ b_j \times N_{emp,j}^\beta}{f(d_{i,j})}} \end{aligned} \tag{4}
\Sigma_j T_{i,j} est généralement directement observé ou estimé lors de l’étape de génération dans les approches dites à 4 étapes. C’est le nombre de départs depuis le point i et il est proportionnel aux nombre d’actifs résidant en i. De la même façon on peut écrire pour b_j une expression symétrique de celle de a_i, qui fait intervenir \Sigma_i T_{i,j} qui est également observée ou estimé auparavant. C’est le nombre de trajets convergeant vers le point d’arrivée j, qui est proportionnel au nombre d’emplois en j.
\begin{aligned} b_j &{}= \frac {\Sigma_i T_{i,j}} {\Sigma_i \frac {a_i \times N_{hab, i}^\alpha \times N_{emp, j}^\beta} {f(d_{i,j})}} \\ &{}= \frac{N_{emp, j}^{1-\beta}}{\Sigma_i \frac{a_i \times N_{hab,i}^{\alpha}}{f(d_{i,j})}} \end{aligned} \tag{5}
La valeur de a_i, pour un i donné, dépend de l’évaluation de tous les b_j et réciproquement l’évaluation de chaque b_j dépend de celle de tous les a_i. On peut estimer ces coefficients par itérations successives et espérer atteindre de cette manière un point fixe, éventuellement unique à une constante multiplicative près. Des algorithmes de résolution ont donc été proposés dans les principaux manuels. L’application de tels algorithmes (comme celui de Furness, Dios Ortúzar et Willumsen (2011), p. 192) modifie le résultat proposé par l’expression du modèle gravitaire équation 2, au risque d’en trahir la logique et les justifications initiales. En effet, les a_i et b_j sont des modificateurs des masses d’actifs et d’emplois. Pour faire fonctionner le modèle gravitaire, il faut « tricher » sur les masses. En outre, la multiplicité des solutions et le choix retenu par l’algorithme demeure un angle mort de ces méthodes.
La procédure de respect des marges aurait pu être formulée différemment, par exemple en utilisant des corrections additives au lieu de corrections multiplicatives ou une combinaison d’additivité et de multiplicativité. Dans tous les cas, rien ne garantit l’existence d’une solution unique et compréhensible. En toute généralité, ces procédures peuvent conduire à des équilibres multiples que l’algorithme de résolution va sélectionner sans que l’on puisse justifier quoi que ce soit. Mais surtout, chacune de ces procédures manque de fondements théoriques : les a_i et b_j ne sont jamais que des « patchs » ; ils ne correspondent à aucune caractéristique interprétable de la zone géographique étudiée.
Le respect de la contrainte aux marges est le pendant global de la contrainte locale de séparabilité. Ces deux propriétés illustrent l’incapacité du modèle gravitaire simple à respecter les aspects fondamentaux du problème. La « plasticité » opérationnelle du modèle gravitaire permet de l’appliquer à des observations en respectant les contraintes observées tout en laissant croire qu’un fondement théorique continue de justifier les opérations. Aussi l’approche gravitaire est-elle largement reprise dans des modèles appliquées (notamment les modèles Land Use Transport Interaction) en dépit de ses défauts majeurs, peut-être faute de mieux. Mais le décalage avec les données rend urgent de dépasser cette approche qui survit en se transformant en boîte noire.
2.2 Une première alternative : le modèle radiatif
Le modèle radiatif est l’une des rares alternatives au modèle gravitaire (Dios Ortúzar et Willumsen, 2011). Il reprend les intuitions de Stouffer (1940) et du modèle des « intervening opportunities », dont la logique est la suivante : un migrant prévoit d’aller dans un endroit distant mais trouve en chemin des opportunités ; il s’interrompt alors en chemin. Cette distraction de son objectif initial est le résultat des opportunités rencontrées en chemins, « intervenantes ». La différence avec le modèle gravitaire est que ce n’est pas la distance qui détermine la destination, mais le nombre de rencontres. La distance et la structure géographique continuent de peser indirectement sur le choix des destinations puisque plus le migrant parcourt une grande distance, plus il a de chances de rencontrer des opportunités. La modélisation initiale de Stouffer souffre toutefois de quelques défauts2 et ne résout pas les questions de capacité ou de respect des contraintes sur les marges. Mais elle ouvre une autre perspective, où le rôle de la distance est médiatisé par le nombre d’opportunités rencontré, ce qui répond avec élégance aux insuffisances de l’analogie gravitaire.
2 Notamment des défauts dans la formalisation qui repose sur une série d’approximation pas toujours explicitées et qui rend le modèle peu manipulable.
3 La notion d’accessibilité a probablement été introduite par Hansen (1959). Pirie (1979) en propose une revue de la littérature. G. Koening (Koenig, 1974, 1980) l’a développée théoriquement et appliquée à la France. Poulit (2005) fait un récit passionnant de l’application par le corps des Ponts et Chaussées en France des annees 1970 aux années 1990.
Avec Stouffer, c’est ainsi une autre métrique qui est proposée en lieu et place de la simple distance spatiale. Elle est liée à la notion d’accessibilité3, c’est-à-dire au nombre d’emplois (et plus généralement d’opportunités) auxquels à accès un individu pour un temps de trajet ou une distance maximaux fixés. Un emploi apparaît ainsi d’autant plus « éloigné » d’un individu qu’il y a d’emplois plus proches de lui. Le modèle gravitaire posait que les individus font une grande différence entre le cas où le deuxième emploi disponible est à 500 m et celui où cet emploi est à 1 km. Dans la nouvelle perspective, il n’y a pas de différence car il s’agit toujours du second emploi rencontré. Autrement dit, la distance est relativisée par la prise en compte du milieu qui est traversé. Plus le milieu est riche en opportunités, moins il est nécessaire d’aller loin et, inversement, plus le milieu est désert, plus il faut se résoudre à aller loin. Ce modèle a connu de nombreuses applications, notamment à Chicago (Ruiter, 1967).
La proposition de Simini et al. (2012) répond à certaines failles de Stouffer (1940) en proposant un modèle inspiré de la physique des radiations. Celui-ci décrit l’émission de particules et leur absorption par le milieu qu’elle traverse. L’intuition est la même que celle de Stouffer (1940) : tant qu’une particule ne rencontre pas d’obstacle, elle poursuit son chemin. Elle ne s’arrête qu’en rencontrant un site qui peut l’absorber, selon un certaine probabilité. Plus le milieu est dense en obstacles, plus la particule a des chances de s’arrêter. Dans ce modèle, la distribution des distances parcourues dépend du milieu et de la quantité de sites d’absorption rencontrés.
Plus précisément, dans le modèle de radiation, chaque particule – ou individu – est tirée aléatoirement d’une distribution de probabilité avec une caractéristique z. Chaque point d’absorption, qui représente un lieu possible de travail, possède une masse d’emploi n_i et se voit attribuer une caractéristique z_i qui est aléatoire. Les lieux possibles sont classés par ordre de distance, comme dans le modèle de Stouffer (1940) et la particule les rencontre dans cet ordre. Le tirage de z_i est construit en tirant n_i fois des z dans la distribution de probabilité et en prenant le maximum de ces z. Plus la masse est grande en i, plus le z_{max} sera grand. La particule émise est absorbée si son z est plus petit que z_i. Pour représenter que la particule sera émise si elle n’est pas absorbée par son point de départ, son propre z est tiré par la même méthode, c’est-à-dire le maximum de m_i tirages où m_i est la masse d’opportunités en i.
Le résultat principal de Simini et al. (2012) est particulièrement élégant. La valeur moyenne (notée \langle T_{i,j}\rangle ) des trajets partant de i et allant en j a une expression qui ne dépend pas de la distribution de probabilité des z. Elle prend l’expression suivante, où s_{i,j}=\Sigma_{k \in (i \rightarrow j)^*} n_k est la somme des opportunités entre i (non inclus) et j (non inclus) :
\langle T_{i,j}\rangle = T_i \times \frac {m_i \times n_j}{(m_i + s_{i,j}) \times (m_i + n_i +s_{i,j})} \tag{6}
A partir d’hypothèses générales assez simples, on obtient une formulation qui s’apparente à celle du modèle gravitaire en remplaçant la distance par l’accumulation des opportunités entre deux points, dès lors que les opportunités sont classées dans l’ordre des distances. Cette formulation respecte autant que le modèle gravitaire le premier principe de Tobler, mais elle repose sur des hypothèses explicites et permet de mieux représenter les phénomènes déjà évoqués. Un départ dans une zone peu dense produira des trajets plus longs pour trouver un nombre équivalent d’opportunités à des trajets plus courts dans une zone dense. De plus, aucune étape de « normalisation » ad hoc n’est requise et le modèle est probabiliste, ce qui permet de produire des marges d’erreurs et des tests empiriques.
Les applications du modèle radiatif à des données diverses (mouvements pendulaires travail-domicile, appels téléphoniques, migrations, logistique) produisent des distributions de trajets plus proches des données que le modèle gravitaire, mettant à mal la croyance selon lequel le modèle gravitaire serait un « bon » modèle, validé par les données.
On notera que le modèle de Simini et al. (2012) admet comme cas limite, sous certaines hypothèses de densité des emplois, le modèle gravitaire. En effet, lorsque la densité d’emplois est uniforme, l’accumulation des opportunités est proportionnelle à la surface et la moyenne de trajets entre i et j est une fonction en 1/r^4 (voir aussi Ruiter (1967)). Ce cas limite montre sous quelle condition (très particulière) le modèle gravitaire peut être valide. Ce cas limite montre également que la forme fonctionnelle employée dans le modèle gravitaire dépend fortement de la distribution de la densité des opportunités, c’est-à-dire les effets du voisinage. Et c’est bien là un des éléments qui manque au modèle gravitaire.
Il subsiste deux défauts au modèle radiatif de Simini et al. (2012). Le premier est le pendant de son élégance : il n’y a pas de paramètres pour l’ajuster, ce qui limite les capacités du modèle à rendre compte de la richesses des données. L’élégant calcul de la moyenne des trajets n’est valide que lorsque le processus sous-jacent suit parfaitement l’hypothèse des auteurs. Or, si l’on veut un modèle de base simple et clair sur le plan conceptuel, on veut aussi pouvoir enrichir le modèle avec des paramètres qui auraient du sens en regard de la richesse des données. Or la seule proposition qu’ils font dans ce sens consiste à introduire un \varepsilon pour modifier le poids du point de départ dans le choix des trajets. Ceci ne répond que très partiellement à ce que l’on souhaiterait. A cet égard, le modèle gravitaire et encore plus le modèle de Fotheringham (voir encadré) sont richement dotés en paramètres, ce qui permet de les ajuster sur les données, au risque toutefois d’un biais lié à la mauvaise définition des paramètres du modèle qui peuvent « attraper » tout ce qui n’a pas été explicité.
Le second défaut est que le modèle ne respecte pas les contraintes aux marges pour les destinations. Dans l’équation 6 le terme T_i permet de caler le modèle sur le nombre de départs de i. En revanche, il n’existe pas de pendant pour se caler sur les destinations j et il n’est donc pas possible au modèle de tenir compte d’une contrainte capacitaire : un nombre de particules supérieur au nombre d’emplois peuvent être absorbées en j. Là aussi, le modèle gravitaire peut passer par dessus ce problème par l’application de procédure de contrainte, qui pourrait aussi bien être appliquées au modèle de Simini et al. (2012). Mais ici encore on perd en route la possibilité d’interpréter ce que produit cette procédure de respect des contraintes.
3 MEAPS : un Modèle Ergodique d’Absorption avec Priorité et Saturation
Nous proposons maintenant une version étendue et remaniée de l’approche de Stouffer (1940) qui répond aux critiques que nous faisons au modèle de Simini et al. (2012). Dans cette section, nous présentons le modèle dans sa forme plus simple avant d’en exposer les extensions les plus directes. Des simulations synthétiques section 4 permettent alors d’apprécier les grandes lignes du fonctionnement de ce modèle. Nous discutons ensuite des procédures d’estimation envisageables ainsi que du développement de mesures issues de ce modèle.
3.1 Rang, choix des destinations et absorption
On considère I individus et J emplois4 localisés sur un territoire. Ces localisations sont fixes et exogènes, ce qui signifie que l’on ne s’intéresse pas au problème de choix de localisation. Non que ce choix ne soit pas important, mais nous nous intéressons à la distribution des trajets, une fois fixées les localisations. L’idée est que pour déterminer le choix de localisation, il faudra prendre en compte ce que la distribution des trajets, leur longueur ou leur coût généralisé nous apprend.
4 Dans ce qui suit on regarde la relation entre résident et emploi ce qui suggère les mobilités domicile travail. C’est principalement pour fixer les idées, mais la relation entre résident et tout type d’aménités peut être abordée de la même façon. Il est également possible de décliner les résident selon des caractéristiques observables et d’indexer le modèle par ces catégories.
On suppose que toutes les localisations sont séparées et qu’il n’y a donc qu’un individu ou qu’un emploi par localisation (les emplois et les individus peuvent être au même endroit). Chaque individu i classe par ordre de distance croissante les J emplois et les examine dans cet ordre. Il a une probabilité p_a de prendre un emploi (tous les emplois sont similaires et ont la même probabilité d’être pris). Tant qu’il ne prend pas d’emplois, l’individu continue sa recherche en passant à l’emploi suivant le plus proche (de son point de départ). La probabilité d’occuper l’emploi j est donc égale à la probabilité de ne pas occuper les emplois plus proches multipliée par la probabilité p_a d’occuper le poste j. En notant r_{i}(j) le rang de l’emploi j dans le classement des distances depuis i, on peut écrire \bar F(j) la probabilité de dépasser le j^{ème} élément :
\bar F(j)=(1-p_a)^{r_i(j)} \tag{7}
On définit également la probabilité de fuite de la zone considérée. Cette probabilité est celle qu’un individu ne trouve pas parmi les J emplois celui qui lui convient et donc qu’il renonce ou cherche plus loin. En supposant pour le moment que cette probabilité est la même pour tous les individus, p_f, on peut déterminer p_a :
p_a = 1-(p_f)^{1/J} \tag{8}
La probabilité P_i(j) de i de s’arrêter en j est :
P_i(j) = (1-p_a)^{r_i(j)-1} \times p_a = {p_f}^{\frac {r_i(j)-1} {J}} \times (1-{p_f}^{1/J}) \tag{9}
Cette expression définit donc la probabilité pour un individu i d’occuper l’emploi j comme une fonction de la probabilité de fuite, le rang de l’emploi et le nombre total d’emploi. La rang de j n’est autre que le nombre d’opportunités cumulées du point de départ de i jusqu’à j et remplace la distance, comme dans les expressions de Stouffer (1940) ou de Simini et al. (2012). Ce nombre n’est autre que l’accessibilité aux emplois de l’individu i dans un cercle de rayon [ij], que ce rayon soit défini en utilisant une distance euclidienne ou d’autres mesures comme le temps de parcours. On notera que l’on considère ici que les emplois sont identiques ou, du moins, parfaitement substituables pour l’individu.
Chaque emploi a été supposé distinct spatialement des autres. Dans le cas où les emplois ne seraient pas séparés et pourraient s’accumuler en un point ou au sein d’un carreau, la formalisation ne change pas – c’est la propriété de séparabilité évoquée plus haut. La probabilité que l’on s’arrête dans le carreau c_d situé à une distance d de i où se trouvent k emplois se déduit de l’équation 7 puisque les k emplois ont des rangs successifs. En notant s_i(d)=\sum _{j/d_{i,j}<d}1 le cumul (i.e.l’accessibilité) de tous les emplois qui sont à une distance strictement inférieure à celle du carreau considéré pour i (et donc à l’exclusion des k emplois du le carreau c_d), on a :
P_i(i\in c_d) = {p_f}^{s_i(d)/J}\times(1-{p_f}^{ k/J}) \tag{10}
En prenant un développement limité au 1er ordre de cette expression (sous l’hypothèse que k est petit devant le nombre total d’opportunités J) , on obtient, en notant \mu=\frac{-log(p_f)}{J} :
P_i(i\in c_d) \approx k\times \mu \times e^{-\mu \times s_i(d)} \tag{11}
Cette expression fait apparaître clairement le cœur du modèle. La proportion d’emplois venant de i dans le carreau est une fonction des emplois dans le carreau multiplié par l’accessibilité jusqu’à ce carreau de i.
Lorsque la densité des emplois est constante sur un plan, s_i(d) est proportionnel à la surface et le modèle devient une fonction de la distance avec un terme en e^{-r^2/\rho^2}. Ici aussi, le comportement de notre modèle rejoint, sous cette condition très particulière d’une répartition homogène des opportunités, celui proposé pour un modèle gravitaire, lorsque celui-ci est spécifié avec une fonction de distance en e^{r/\rho}. La forme favorite du modèle gravitaire se justifierait pour une répartition homogène des opportunités le long d’une droite5. Ce résultat diffère de celui de Simini et al. (2012), qui trouvaient un comportement asymptotique en 1/r^4.
5 La littérature sur le commerce international fait un grand usage du modèle gravitaire et on y trouve des développements très riches. Le problème du commerce international est un peu différent de celui de l’analyse des distribution de déplacement parce qu’on observe les flux bilatéraux par produit de façon répétée entre les pays. On dispose ainsi d’une grande quantité d’informations à relier entre elles par la représentation gravitaire. La question du transport est différente en ce que la distance entre origines et destination est bien connue, mais que les trajets bilatéraux ne le sont pas. On dispose en revanche d’information sur la distribution des trajets en fonction de leur distance, de leur motif et des modes employés.
Tout comme dans le modèle de Simini et al. (2012), le résultat est sans paramètre, parce que la probabilité de fuite est entièrement déterminée par la contrainte en ligne (l’individu i a une espérance égale à 1 - p_f de trouver un emploi dans la zone considérée).
3.2 Saturation et priorité
Il reste encore à prendre en compte la contrainte en colonne, c’est-à-dire le fait que chaque emploi peut être pourvu une fois et une seule. Au lieu d’un ajustement ad hoc qui tombe de nulle part, nous proposons le mécanisme suivant de remplissage des emplois : chaque individu i est classé selon un ordre de priorité. L’individu au premier rang est confronté à l’ensemble des emplois et nous calculons ses probabilités de prendre un emploi j par la formule précédente (équation 9). Les emplois sont alors partiellement remplis à proportion de ces probabilités6. Le deuxième individu est traité de la même manière, et ainsi de suite, jusqu’à ce qu’un ou plusieurs emplois soient totalement pourvu (lorsque la somme des probabilités dépasse tout juste 1). On retire alors ces emplois de la liste des choix possibles et on continue l’affectation pour les individus suivants sur la liste réduite. A chaque individu ajouté, on peut être amené à retirer d’autres emplois de la liste de recherche.
6 En toute rigueur, les probabilités ne s’additionnent pas si simplement et un traitement exact exigerait de tenir compte de probabilités conditionnelles au fait que tel emploi a été pris, ou non, auparavant. La procédure décrite ici est une simplification, en subsituant aux probabilités conditionnelles des espérances.
A la fin de ce processus, tous les individus ont des emplois (à p_f près) et tous les emplois sont pourvus dès lors que l’on pose I \times (1 - p_f) = J. Cette attribution avec priorité est Pareto-optimale. Il n’est pas possible d’augmenter la satisfaction d’un individu sans dégrader celle d’un autre. A chaque étape, chaque individu réalise ses choix sans contrainte autre que l’éventuelle saturation provoquée par ses prédécesseurs. Pour augmenter sa satisfaction, c’est-à-dire lui permettre d’occuper en probabilité un emploi mieux classé pour lui, il faudrait dégrader la situation d’un prédécesseur en lui attribuant un emploi plus éloigné pour lui. Cette procédure d’affectation avantage les premiers du classement, mais tient compte des choix de chacun.
Formellement, on note \phi_u(i,j) la probabilité de disponibilité (\phi vaut 0 si l’emploi est complètement pris) de l’emploi j pour un ordre de priorité donné u au moment où l’individu i doit choisir. La probabilité de cet individu i de prendre l’emploi j s’écrit alors :
P_{u, i}(j) = \lambda_{u,i}.\phi_u(i,j). p_a \prod_{l=1}^{r_i(j)-1}(1-\lambda_{u,i}. \phi_u(i,r^{-1}(l)).p_a) \tag{12}
Cette expression est rendue complexe par la nécessité de parcourir les emplois dans l’ordre qui correspond à chaque individu. La probabilité p_a doit alors être calculée pour que le taux de fuite de i soit inchangé. On suppose que les emplois restants demeurent parfaitement substituables tout au long du processus d’affectation. La probabilité de chacun est donc identique et ajustée d’un facteur multiplicatif \lambda_{u,i}. Le terme \lambda_{u,i} découle ainsi de l’indisponibilité potentielle des emplois. Lorsqu’un emploi est indisponible, l’individu i, lorsque c’est son tour de choisir, connait ses cibles potentielles. Il ajuste donc sa probabilité d’absorption de façon à respecter la probabilité de fuite. C’est de cette manière que nous respectons la contrainte en ligne, qui s’exprime par l’équation 13 ci-dessous. Ceci signifie qu’un individu a d’autant plus de chances d’accepter un emploi qu’il reste peu de choix.
Une autre solution serait de considérer que la probabilité de fuite n’est pas conservée et que les indisponibilités se traduisent par une fuite plus élevée. On peut tout à fait envisager des solutions plus complexes. Nous nous en tenons pour l’instant au cas simple où tous les individus ont la même chance de travailler dans la zone considérée7. Sous cette hypothèse de conservation de la probabilité de fuite, on a :
7 En pratique, pour éviter les effets de bord, il faut choisir une zone d’emplois plus grande que la zone des résidents.
\forall i, \prod_{j=1} ^{J} (1-\lambda_{u,i} \times \phi_u(i,j) \times p_{a})= p_f \tag{13}
La solution de cette équation est celle d’un polynôme en \lambda_{u,i} d’un ordre élevé. Il y a possiblement plusieurs solutions, mais il est nécessaire que \lambda_{u,i} \times p_a \in ]0;1[, ce qui réduit le nombre de solutions admissibles. Pour un i donné, on peut en produire une solution approchée par un développement limité à l’ordre 1 en prenant le log de l’équation 13 :
p_{a} \times \lambda_{u,i} = \frac {-log(p_f)}{\sum_{j=1} ^{J} \phi_u(i,j)} \tag{14}
On peut vérifier que 0<\lambda_{u,i}\times p_a<1 lorsque J est assez grand et que le nombre d’emplois restant demeure élevé (en probabilité) par rapport à -log(p_f).
3.3 Ergodicité
Chaque ordre de priorité u définit une trajectoire possible d’affectation des emplois aux résidents (ou l’inverse). On aboutit à chaque fois à un état possible de l’appariement résidents-emplois d’où l’on déduit les trajets professionnels. Bien entendu, le résultat final dépend de l’ordre de priorité choisi. Pour s’en affranchir, la stratégie usuelle en physique statistique consiste à réitérer la procédure pour tous les ordres possibles de priorité et à considérer la moyenne des résultats obtenus sur les I! ordres de priorité possibles.
L’hypothèse ergodique consiste ici à soutenir que cette moyenne sur tous ces ordres de priorité est proche du régime permanent des trajets professionnels sur la zone considérée.
La première grandeur que nous moyennons sur les ordres u est la variable de disponibilités \phi_u(i,j) de l’emploi j pour le résident i. Cette moyenne \langle\phi\rangle_u(n,j) correspond à la probabilité de disponibilité de l’emploi j pour n’importe quel résident après que n résidents occupent d’ores et déjà un emploi ou ont fuit la zone. Cette grandeur ne dépend pas de i, mais uniquement du nombre de résidents déjà positionnés.
Une deuxième grandeur nous sera utile. Il s’agit de l’accessibilité moyenne aux emplois disponibles. On peut noter A_n(i,k) le cumul des emplois qui restent disponibles pour i lorsque n résidents se sont d’ores et déjà positionnés, en comptant les emplois depuis le plus proche de i jusqu’au k^{ième} le plus proche. La grandeur qui nous intéresse est la moyenne sur tous les n possibles, soit :
\langle A \rangle_n(i,k) = \langle\sum_{j, r_i(j)\leq k} \langle \phi \rangle_u(n,j) \rangle _n \tag{15}
La particularité de cette accessibilité est qu’à mesure que les emplois sont pris (lorsque n s’accroît), l’accessibilité se restreint puisqu’elle ne retient que la part encore disponible des emplois proches.
Comme précédemment, nous considérons que la probabilité de fuite d’un individu est une constante. Dans ce cas, la probabilité d’absorption va augmenter au fur et à mesure que les emplois sont pris : moins il reste d’emplois disponibles, plus un résident est prêt à accepter ceux qui restent. La probabilité P_a va donc dépendre de n et s’écrire ici P_{a,n}. Pour un n donné, on a :
P_f=\prod_{k=1}^J(1-P_{a,n}\times \langle \phi \rangle_u(n, r_i^{-1}(k)) \tag{16}
En passant en log et en effectuant un développement limité, on obtient :
log(P_f)=-P_{a,n}\times\sum_{k=1}^J \langle \phi \rangle_u(n,r_i(k))=-P_{a,n}\times(J-(1-P_f)\times n) \tag{17}
Nous avons alors tous les éléments pour calculer la probabilité P_n(i,j) que le résident i prenne l’emploi j après que n résidents se sont déjà positionnés (cf. équation 9). En passant alors en log, on a :
log(P_n(i,j))=log(P_{a,n})+log(\langle\phi \rangle_u(n,j))+\sum_{k=1}^{r_i^{-1}(j)}log(1-P_{a,n}\times \langle \phi \rangle_u(n,r_i(k)) \tag{18}
En faisant un développement limité du dernier terme puis la moyenne sur les n, il en découle :
log(P_{ij})\approx\langle log(P_{a,n})\rangle _n+\langle\langle\phi\rangle_u(n,j)\rangle_n + \langle A\rangle_n(i, r_i(j)) \tag{19}
La probabilité P_{ij} s’écrit donc à partir de la probabilité moyenne d’absorption, de l’espérance que l’emploi j est disponible et de l’accessibilité moyenne. Sur le plan conceptuel, c’est tout à fait satisfaisant et compréhensible. Il reste que ces grandeurs ne peuvent pas être calculées directement ; il faut en passer par des simulations.
3.4 Hétérogénéité de la fuite et de l’absorption
Nous avons considéré jusqu’à présent le cas où les individus et les emplois étaient parfaitement substituables. Cela simplifie le modèle et permet une résolution explicite. Il est cependant possible de complexifier le modèle en introduisant des paramètres interprétables qui permettent une meilleure prédiction et l’extraction d’informations des données.
Tout d’abord, le paramètre de fuite peut être spécifique à chaque commune de résidents ou chaque type de résidents. Par exemple, le recensement nous permet de mesurer la proportion d’individu, par commune, qui ont un emploi à plus de 100km de leur domicile. Cette proportion est faible (\le5\% pour une région comme celle étudiée dans l’application à la Rochelle (Parodi et Timbeau, 2024b)) mais peut varier d’une commune à l’autre pour diverses raisons : les communes ne sont pas toutes aussi bien desservies ; certaines se trouvent à la périphérie de la zone d’étude ; les caractéristiques moyennes des résidents varient d’une commune à l’autre… Le modèle peut sans difficulté prendre en compte une probabilité de fuite p_{f,i} pour chaque individu.
Ensuite, le paramètre d’absorption était jusqu’à maintenant identique pour tous les emplois et tous les individus. On peut le rendre dépendant des emplois, p_{a,j}, pour marquer un effet fixe spécifique à des emplois, de manière à souligner l’attractivité de telle ou telle zone d’emplois. Le recensement nous donne quelques informations sur les trajets professionnels de commune à commune et, donc, sur l’attractivité différentielle entre communes. D’autres données pourraient nous informer à un niveau infra-communal. On pourrait aussi vouloir faire dépendre la probabilité d’absorption de caractéristiques observables des emplois. Des emplois dans une zone dense en emploi peuvent, au-delà de l’effet masse déjà pris en compte, être plus attractifs que des emplois isolés. Dans ce cas, l’absorption dépend de caractéristiques X observées et en spécifiant la forme fonctionnelle de p_a(X) on peut l’estimer de façon à mieux reproduire l’information sur la distribution des déplacements.
Le modèle présenté est suffisamment flexible pour pouvoir rendre compte de phénomènes plus complexes afin de, à la fois, pouvoir exploiter des données riches et modéliser des comportements (de fuite, d’absorption) qui semblent avoir un sens. Si au lieu d’apparier les individus et les emplois, on s’intéresse au cas du choix des écoles, on peut imaginer que l’absorption de l’école la plus proche est élevée tandis que celles de rang supérieur s’effondrent rapidement. Si l’individu est indifférent aux caractéristiques des écoles, hors leur emplacement, il prend l’école la plus proche. Le refus de cette première école peut s’expliquer par une exigence parentale non observable, qui se traduit par une distance parcourue plus élevée. Mais le modèle de base rendant compte d’une baisse de l’absorption au-delà du premier rang sera vraisemblablement assez bon8. Il est possible aussi d’augmenter ou de diminuer l’absorption de certaines paires résidents-écoles, ce qui est une manière d’introduire par exemple les informations sur la carte scolaire.
8 De façon plus générale, on peut spécifier une loi de la probabilité d’absorption quelconque qui doit vérifier que \sum_{k=1,J} p_{i,r_i(k)} = p_{f,i} pour tout i. Toute paramétrisation de cette loi de probabilité peut alors être simulée et ajustée sur des données. Si les paramètres ont une interprétation théorique, on peut alors les identifier.
On peut ainsi modifier les probabilités d’absorption en donnant à un groupe particulier de paires individus emplois plus ou moins de chances d’être absorbé. En jouant sur les groupes qui partitionnent les paires individus \times emplois on peut augmenter ou réduire le nombre de degré de liberté du système. Lorsque seule la probabilité d’absorption est un paramètre, le nombre de degré de liberté est diminué de 1 et le paramètre p est déterminé par la condition d’égalité entre le nombre d’emplois pourvus et d’individus. Si on dispose d’une information sur la probabilité de fuite par individu ou par groupe d’individus, le nombre de degré de liberté peut être accru par une probabilité de fuite différenciée selon ces groupes. On peut encore accroître le nombre de degré de liberté en croisant une probabilité d’absorption par groupes d’emplois et groupes d’individus. Le choix de la spécification dépendra de ce que l’on souhaite réaliser et du problème considéré. On verra dans l’estimation à la Rochelle une application en recourant à un grand nombre de degrés de liberté afin d’ajuster le modèle sur des données détaillées (donnant pour des paires commune de résidence \times commune d’emploi une observation des flux de mobilité professionnels). Nous y montrons aussi une détermination parcimonieuse des coefficients correcteurs afin de pouvoir extraire une information pertinente des données de flux entre communes et de pouvoir comparer le pouvoir prédictif de MEAPS à celui d’un modèle gravitaire, à degré de liberté égal.
En indexant par i les probabilités de fuite p_{f,i} et par i,j les coefficients correcteurs \lambda_{i,j}, les équations principales du modèle deviennent :
P_{i, u}(j) = \lambda_{i,j} . p_{a} \prod _{l=1} ^{r_{u(i)}(j)-1} {[1-\lambda_{i,r_{u(i)}(l)}. p_{a}.\phi_u(i,r_{u(i)}^{-1}(l))]} \tag{20}
\prod _{l=1} ^{J} {[1-\lambda_{i,r_{u(i)}(l)}.p_{a}.\phi_u(i,r_{u(i)}^{-1}(l))]}= p_{f,i} \tag{21}
Il n’est pas possible de donner une forme réduite de cette dernière expression. En revanche, elle est calculable numériquement pour chaque u, i et j en fonction des hypothèses du modèle (p_{f,i}, p_{a,j}, la structure spatiale des résidents et des emplois) et sert de base à l’algorithme de calcul employé dans les simulations présentées dans la partie section 49.
9 Cette expression est implémentée dans le package R {rmeaps} disponible dans le dépôt github github.com/maxime2506/rmeaps et s’installe dans R par devtools::install_github("maxime2506/rmeaps"). Il est utile de disposer d’un compilateur qui accepte OpenMP, ce qui demande quelques manipulations sur MacOS.
Le modèle ainsi construit est flexible puisqu’on peut spécifier des processus de fuite (contrainte en ligne équivalente à la contrainte 4) et des processus d’absorption qui respecte la contrainte de saturation des emplois (contrainte en ligne équivalente à la contrainte 5) par le processus de priorité décrit en section 3.2. Le parcours de toutes les permutations possibles permet de s’affranchir d’un ordre de priorité particulier et de définir une solution moyenne au processus. Lorsqu’on analyse le problème avec une grille de taille finie (ou de taille inférieure au nombre J d’opportunités), on peut conjecturer un comportement ergodique des quantités moyennes prédites par le modèle. On résout de cette façon explicitement le problème de contrainte aux marges du modèle gravitaire ou du modèle radiatif.
Pour étudier quelques-unes des propriétés du modèle, nous proposons ici d’explorer son comportement sur des données synthétiques. Les données synthétiques, générées de façon explicites, permettent de contrôler les variations de paramètres afin d’en isoler les conséquences. Ces simulations ne prétendent ni à l’exhaustivité ni à la démonstration, mais peuvent servir à appuyer l’intuition. L’ensemble de la partie sur les simulations synthétiques est exécutable au sens de Lasser (2020). Les codes nécessaires à la reproduction de ces simulations et des graphiques associés sont disponibles sur github.com/xtimbeau/meaps et exécutables librement.
4 Simulations synthétiques
4.1 Trois pôles en centre et satellites
Nous construisons un territoire abstrait composé d’un « centre ville » et de « deux périphéries » (figure 1). Cette configuration arbitraire nous permet d’évaluer MEAPS en simulant les trajets et leur distribution. Chaque individu et chaque emploi sont localisés, distinctement les uns des autres, ce qui permet de calculer des distances euclidiennes entre chaque habitant et chaque emploi et d’en déduire un classement pour chaque habitant sans ambiguïté des emplois en fonction de leur éloignement. Tous les emplois sont considérés comme substituables et on suppose une probabilité de fuite identique de 10% pour tous les individus. Les distances entre les pôles sont données dans le tableau 1 (dans une unité quelconque).
Pour assurer l’égalité entre demandes et offres d’emploi, on tire aléatoirement 4 500 emplois. Les trois pôles d’emplois ont les mêmes centres que les pôles d’habitation, mais ont une répartition plus resserrée que pour les habitants. Comme indiqué sur la figure 1, les tâches d’emplois sont respectivement localisés autour des mêmes centres que les zones d’habitation. Les pôles périphériques comportent moins d’emplois (15% chacun) que le pôle central (70% de l’emploi total) pour rendre compte d’une structuration habituelle où on trouve dans les pôles périphériques avant tout des emplois liés aux services fournis aux résidents (comme des commerces ou des écoles) tandis que la zone d’activité centrale rassemble une plus large palette d’emplois, en plus grand nombre. Nous ne faisons aucune distinction de productivité ou de qualification nécessaire pour les emplois. Cette hypothèse simplifie la simulation du modèle, mais rien n’empêche de distinguer des catégories d’emplois, des catégories d’habitants ni d’introduire des éléments de choix entre distance et nature de l’emploi. Nous ne considérons pas ici le choix de la localisation et considérons toutes les localisations comme exogènes.
Dans l’analyse statistique qui suit, on procédera à une agrégation spatiale en pavant le plan où sont localisés les emplois et les habitants par des hexagones adjacents. Ceci correspond à une analyse empirique où les données de localisation sont carroyées.
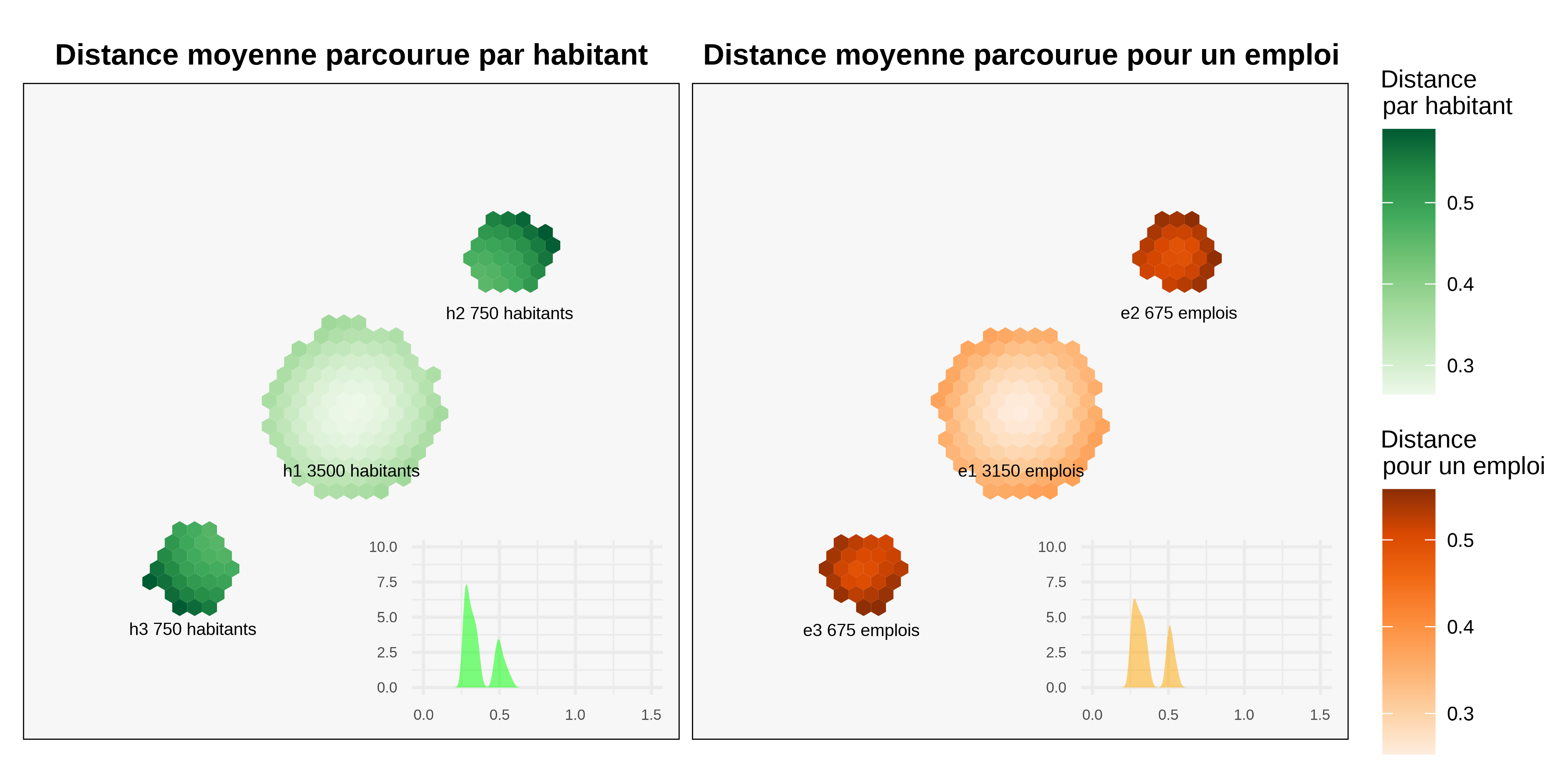
La figure 2 simule MEAPS à partir des données de figure 1. On obtient pour chaque hexagone de résident une valeur moyenne de distance jusqu’à leur emploi. De la même façon, on calcule pour chaque emploi la distance accomplie en moyenne pour l’atteindre.
Cette première représentation graphique permet de voir le fonctionnement du modèle MEAPS. On peut générer une distribution de trajets (dans les vignettes de la figure 2). Comme la majorité des emplois se trouvent dans le pôle central, les distances moyennes pour les habitants y sont plus faibles que dans les autres pôles. Le modèle génère un peu de variance à l’intérieur de chaque pôle. On retrouve l’idée que les hexagones d’habitations les plus excentrées génèrent des distances plus importantes. La distribution des distances moyennes pour atteindre un emploi est plus resserrée que celle des distances parcourues en moyenne par habitant. Les moyennes de ces deux distributions sont égales (par construction).
On peut construire une table des flux entre chaque pôles (tableau 2). Le premier élément est de noter que les contraintes aux marges sont parfaitement respectées, ce qui est le principe de construction de MEAPS, les approximations faites dans l’algorithme de résolution restant ici inférieures à 10^{-5} au moins. Par ailleurs, la table de flux confirme le diagnostic précédent. La plupart des habitants de h1 (78%) se rendent dans g1 (le même pôle donc). Ce taux d’emploi « intrapôle » est de 42% pour les deux autres pôles. Ceci tient au déséquilibre de localisation des emplois et est une propriété souhaitée du modèle. Cela explique en partie la distribution des distances de la mobilité professionnell pour les habitants et également sa « réciproque », lorsqu’on calcule les distances moyenne vers un hexagone d’emplois.
| e1 | e2 | e3 | total | |
|---|---|---|---|---|
| h1 | 2 481 | 335 | 334 | 3 150 |
| h2 | 334 | 290 | 51 | 675 |
| h3 | 334 | 50 | 290 | 675 |
| total | 3 150 | 675 | 675 | 4 500 |
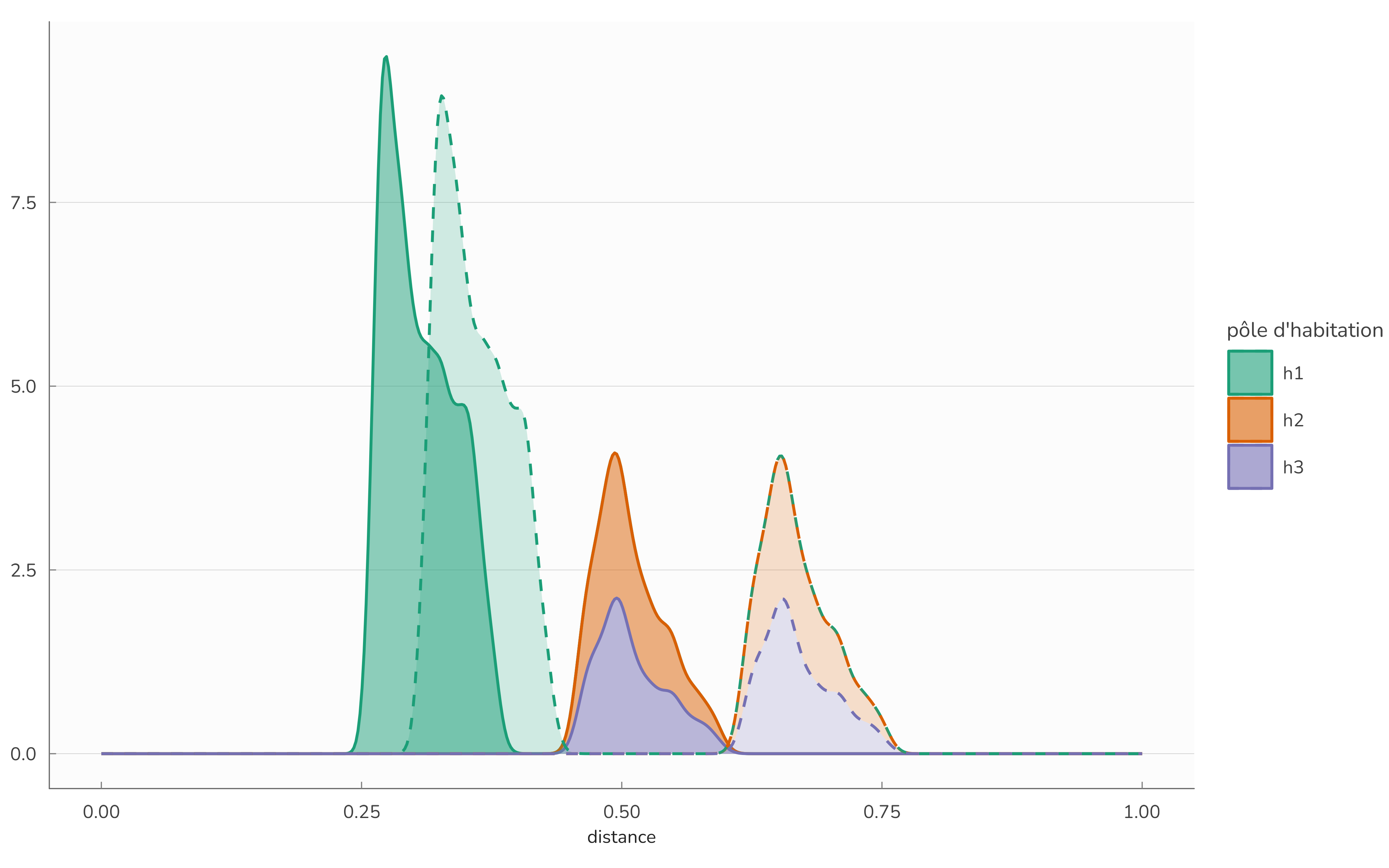
Pour apprécier le comportement du modèle, on peut procéder à une expérience de pensée dans laquelle on éloigne les deux pôles satellites du centre (la distance entre 1 et 2 ou 3 passe de 0.7 à 1.2 dans cette expérience). Le tableau 3 est obtenu en simulant à nouveau le modèle sur cette géographie alternative. Le résultat est identique à la configuration précédente. Ce résultat est conforme à l’intuition et est une propriété souhaitée du modèle. Puisque les ordres de classement ne changent pas (dès lors que les pôles sont assez éloignés et que la configuration demeure symétrique), les rangs ne sont pas modifiés et donc les flux sont inchangés. Les distributions des distances (sortantes et arrivantes) sont largement modifiées, puisque 2 ou 3 sont plus loin de 1, comme l’indique la figure 3. On est tenté de conduire d’autres expériences de pensée pour analyser le comportement du modèle. L’application Shiny accessible à ofce.shinyapps.io/rmeaps permet de conduire toutes ces expériences en utilisant le même code que celui utilisé ici.
| e1 | e2 | e3 | total | |
|---|---|---|---|---|
| h1 | 2 482 | 334 | 334 | 3 150 |
| h2 | 334 | 290 | 51 | 675 |
| h3 | 334 | 51 | 291 | 675 |
| total | 3 150 | 675 | 675 | 4 500 |
4.2 Comparaison avec le modèle gravitaire
Comparer MEAPS au modèle gravitaire permet d’en comprendre les avantages. Pour ce faire, nous simulons un modèle gravitaire à double contrainte équation 3, c’est-à-dire permettant le calage sur les lignes (chaque individu a un emploi) et sur les colonnes (chaque emploi est pourvu). Ce modèle est simulé au niveau désagrégé, c’est-à-dire au niveau de chaque individu et de chaque emploi à partir de la configuration géographique décrite plus haut en section 4.1. La spécification du modèle gravitaire est faite en utilisant comme fonction f l’expression suivante où \delta est un paramètre positif :
f(d) = e^{d/\delta} \tag{22}
Il s’agit d’un choix très commun. Le modèle gravitaire peut être ensuite normalisé en utilisant l’algorithme de Furness (Dios Ortúzar et Willumsen, 2011) dans lequel on normalise d’abord sur les lignes (chaque individu a un emploi et un seul en probabilité, en tenant compte du paramètre de fuite), puis sur les colonnes (chaque emploi est pourvu complètement). On itère ces normalisations en ligne puis en colonne jusqu’à obtenir une matrice de flux stable. Ces normalisations suivent les équation 4 et équation 5.
Ce modèle gravitaire ainsi spécifié est ajusté sur la simulation MEAPS en prenant comme référence les flux du tableau 2, construits par agrégation sur les groupes d’habitants et d’emplois – donc une matrice 3 \times 3. L’ajustement est réalisé en calibrant le paramètre \delta de façon à minimiser l’entropie relative de Kullback-Leitner des distributions agrégées (cette notion d’entropie est détaillée dans le document Estimations à la Rochelle). Le résultat de l’estimation est proposé dans le tableau 4 et correspond à une valeur de \delta \approx 0.68.
| MEAPS Fuite à 10% |
Gravitaire Normalisé, δ = 0.68 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| e1 | e2 | e3 | total | e1 | e2 | e3 | total | |||
| h1 | 2 481 | 335 | 334 | 3 150 | h1 | 2 447 | 352 | 350 | 3 150 | |
| h2 | 334 | 290 | 51 | 675 | h2 | 353 | 286 | 36 | 675 | |
| h3 | 334 | 50 | 290 | 675 | h3 | 350 | 37 | 288 | 675 | |
| total | 3 150 | 675 | 675 | 4 500 | total | 3 150 | 675 | 675 | 4 500 | |
L’ajustement du modèle gravitaire donne un bon résultat. Une des raisons de ce bon résultat découle de la symétrie de la configuration géographique. Les deux satellites sont à même distance du pôle central et la fonction f qui ne dépend que de la distance permet d’assurer une répartition des flux entre chacun des pôles sans trop de difficulté. Si on prend une configuration non symétrique, en éloignant un des deux satellites, l’autre restant à sa place, on obtient un schéma différent, le modèle gravitaire amplifiant les asymétries.
| MEAPS Fuite à 10% |
Gravitaire Normalisé, δ = 0.68 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| e1 | e2 | e3 | total | e1 | e2 | e3 | total | |||
| h1 | 2 482 | 334 | 334 | 3 150 | h1 | 2 581 | 285 | 284 | 3 150 | |
| h2 | 334 | 290 | 51 | 675 | h2 | 286 | 367 | 22 | 675 | |
| h3 | 334 | 51 | 291 | 675 | h3 | 284 | 23 | 369 | 675 | |
| total | 3 150 | 675 | 675 | 4 500 | total | 3 150 | 675 | 675 | 4 500 | |
Le modèle MEAPS conserve une configuration identique dans le cas de pôles satellitaires éloignés du centre, parce que la configuration reste symétrique et qu’aucun rang n’est modifié. En revanche, le modèle gravitaire renvoie une réponse très différente de celle du cas de référence : les habitants des satellites se tournent plus vers les emplois de leur satellite respectif et les flux entre pôles satellites et le pôle central se réduisent. Cette propriété du modèle gravitaire est attendue : la fonction f donne un poids plus faible aux emplois plus distants. A la limite où cet éloignement devient particulièrement grand, les flux entre pôles satellites et le pôle central vont se tarir presque entièrement. Le paramètre estimé sur la simulation MEAPS est de l’ordre de 0.68, ce qui est l’ordre de grandeur du rayon du pôle central (0,5). Pour une distance de quelques fois 0.68, les flux entre pôles seront quasi nul. La réponse de MEAPS parait ici plus adaptée à ce que l’on observe. Lorsque des communes sont satellites d’un pôle central à une distance de quelques dizaines de kilomètres, il existe des flux vers cette commune pour occuper des emplois, et le fait que la commune soit plus éloignée de quelques kilomètres ne tarit pas drastiquement ces flux. On s’attend à une faible sensibilité de la distance à cette échelle. Nous verrons lors de l’application à l’agglomération de la Rochelle, en utilisant des données décrivant les flux entre commune de résidence et commune d’emploi (issues de INSEE (2022)) que MEAPS permet une meilleure représentation de la réalité que le modèle gravitaire.
Si l’on reconduit la procédure d’estimation du paramètre \delta sur la configuration géographique où les pôles satellite sont éloignés on aboutit à \delta \approx 0.95. Cette valeur est très différente du paramètre précédent, ce qui montre à la fois la « plasticité » du modèle gravitaire et son manque de fiabilité, comme si la force « gravitationnelle » pouvait changer du tout au tout à chaque nouvelle donnée (tableau 6).
| MEAPS Fuite à 10% |
Gravitaire Normalisé, δ = 0.95 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| e1 | e2 | e3 | total | e1 | e2 | e3 | total | |||
| h1 | 2 482 | 334 | 334 | 3 150 | h1 | 2 455 | 348 | 347 | 3 150 | |
| h2 | 334 | 290 | 51 | 675 | h2 | 348 | 288 | 39 | 675 | |
| h3 | 334 | 51 | 291 | 675 | h3 | 347 | 39 | 289 | 675 | |
| total | 3 150 | 675 | 675 | 4 500 | total | 3 150 | 675 | 675 | 4 500 | |
4.3 Procédure d’estimation
Il est possible de modifier les pondérations des probabilités d’absorption de façon à modifier la table des flux. Ceci est illustré dans la table suivante où on a doublé pour chacune des 9 paires possibles de zone d’habitation (3) et de zone d’emploi (3) la probabilité relative d’absorption successivement. La configuration géographique est celle de la figure 1, avec un centre et deux satellites. Le centre comporte plus d’emplois que de résidents, ce qui oblige à des flux entrants dans la zone 1 comme indiqués dans la- tableau 2. On parle de doublement relatif de la probabilité, parce que les contraintes de constance de probabilité de fuite et de saturation des emplois imposent une réduction des probabilités d’absorption des autres emplois, ce qui est assuré dans l’algorithme qui implémente MEAPS.
Le tableau 7 décrit les variations de flux par rapport à une situation de référence (celle du tableau 2), arrondi à l’entier le plus proche. Il y a donc 3 \times 3 matrices 3 \times 3. Chacune des sous matrices indique les variations de flux pour chaque paire origine-destination ; il y a 9 possibilités de doublement de la probabilité d’absorption, qui constituent les lignes et les colonnes de la matrice englobante. On notera que les sommes des colonnes et des lignes de chaque sous matrice sont nulles, ce qui indique le respect des contraintes en ligne et en colonne.
Conformément à l’intuition, et malgré les effets induits par le respect des contraintes en ligne et en colonne, on observe bien que la paire zone d’habitation-zone d’emploi qui se voit augmentée en probabilité relative connait des flux supérieurs. Pour compenser ces flux supérieurs, dans la même colonne, c’est-à-dire pour les flux en provenance des autres zones d’habitation, on constate systématiquement une diminution des flux en provenance des autres zones d’habitation. Symétriquement, un accroissement des flux de la zone d’habitation i vers la zone d’emploi j induit toujours une diminution des flux de i vers les autres zones d’emploi.
| e1 | e2 | e3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| e1 | e2 | e3 | e1 | e2 | e3 | e1 | e2 | e3 | ||
| h1 | h1 | 76 | −38 | −38 | −72 | 55 | 17 | −72 | 17 | 55 |
| h2 | −38 | 27 | 11 | 81 | −63 | −18 | −9 | 1 | 8 | |
| h3 | −38 | 11 | 27 | −9 | 8 | 1 | 81 | −18 | −63 | |
| h2 | h1 | −59 | 75 | −15 | 75 | −76 | 1 | 2 | −26 | 24 |
| h2 | 51 | −58 | 7 | −80 | 87 | −7 | 7 | −13 | 5 | |
| h3 | 9 | −17 | 8 | 5 | −11 | 7 | −9 | 39 | −30 | |
| h3 | h1 | −59 | −15 | 75 | 2 | 24 | −26 | 75 | 0 | −76 |
| h2 | 9 | 8 | −17 | −9 | −30 | 39 | 5 | 7 | −12 | |
| h3 | 51 | 7 | −58 | 7 | 5 | −12 | −80 | −7 | 87 | |
| Le tableau représente l’écart entre les flux obtenus pour une probabilité d’absorption doublée pour la zone i d’habitation et la zone j d’emploi, pour chaque paire de zones habitation/emploi. La première matrice en haut à gauche indique donc que le flux entre la zone 1 d’habitation et la zone 1 d’emploi est accru de 76 lorsque la probabilité d’absorption relative est doublée. Pour compenser ce flux plus important entre 1 et 1, le flux en la zone d’habitation 2 et l’emploi 1 est réduit de 38, ce qui implique à son tour que ceux entre 2 et 2 et entre 2 et 3 s’accroissent. | ||||||||||
Une propriété intéressante des matrices du tableau 7 est que les 9 matrices 3 \times 3 forment un espace vectoriel10 de dimension 4. Ceci est attendu, puisque les contraintes réduisent la dimension de 9 (=3\times 3) à 4, puisqu’il y a 3 contraintes dans chaque dimension (lignes et colonnes) et qu’une est redondante (si les somme sur chaque ligne sont nulles, alors la somme de tous les coefficients est nulle et donc si les sommes sur deux colonnes sont nulles, la troisième l’est nécessairement). Cela indique que, au moins localement (au voisinage de la matrice de flux calculée dans le tableau 2), il est possible de modifier les probabilités d’absorption pour atteindre n’importe quelle matrice de flux. A l’approximation linéaire près, il est donc possible de reproduire n’importe quelle structure de flux agrégés par un jeu de paramètres saturant exactement la dimension de cette structure de flux. Cette propriété permet d’envisager différentes approches d’estimations, suivant les données dont on dispose et du nombre de degrés de liberté que l’on est prêt à consacrer à la reproduction des données.
10 Les valeurs propres de la matrice 9 \times 9 constituée des 9 vecteurs colonnes des 9 matrices « dérivées » sont (133.3, 97.3, -28.6, 22.0, 0, 0, 0, 0, 0). Les 5 valeurs propres nulles et les 4 non nulles permettent de conclure que la dimension de l’espace vectoriel engendré par les 9 matrices est 4.
Le temps de calcul peut être assez long du fait de la nécessité de répéter un grand nombre de tirages, mais la section suivante (section 4.4) montre que ce nombre peut rester raisonnable. Une estimation de ce type est mise en oeuvre par une procédure itérative dans le document Estimations à la Rochelle, permettant de reproduire à l’aide de MEAPS les données issues de l’enquête mobilités professionnelles INSEE (2022) avec un schéma de calcul qui peut se mettre facilement en œuvre.
4.4 Ergodicité en pratique
L’utilisation de données synthétiques permet de tester simplement l’hypothèse d’ergodicité. On a conjecturé que les différentes grandeurs moyennes sur les permutations u étaient assimilables à des observations, éventuellement répétées. A ce stade de simulations synthétiques nous ne confrontons pas le modèle à des observations (voir Estimations à la Rochelle), mais nous allons montrer que l’estimation des valeurs moyennes ne demande pas l’examen des I! permutations possibles11 et peut se contenter d’une agrégation spatiale et de quelques tirages de permutations.
11 Par la formule de Stirling log_{10}(I!) \approx (n +1/2)log_{10} n +log_{10}\sqrt{2} - n log_{10}e \approx 5\times10^5 pour I=10^5, ce qui fait un nombre de grande taille.
Pour illustrer cette propriété, nous répétons les simulations du modèle pour plusieurs tirages de priorités (notés u dans la section section 3.3), suivant une méthode de Monte-Carlo. En prenant la moyenne sur un échantillon de u, on peut construire un estimateur des grandeurs moyennes et montrer qu’avec un échantillon petit par rapport à I!, on peut les estimer avec fiabilité et dans un temps raisonnable. Cette propriété sera montrée sur la structure géographique particulière que nous avons synthétisée, sans que cela permette de le généraliser avec certitude. Il existe sans doute des configurations spatiales pathologiques qui contredisent cette conjecture.
La figure 5 illustre les processus stochastiques à l’œuvre dans le modèle et leur résolution par la moyennisation sur les tirages possibles. On applique le modèle en tirant aléatoirement des permutations de priorité entre les résidents. On représente alors pour quelques hexagones d’habitation (tirés au sort) l’ensemble des choix de destination (carroyés dans les hexagones). Le carroyage opère déjà une moyennisation puisque chacun des individus de chaque hexagone a un ordre de priorité différent. On représente alors les quantités d’emplois (la probabilité de choisir un emploi qui se trouve dans l’hexagone d’arrivée). Les lignes blanches illustrent la dépendance au tirage de priorité. Mais au bout de quelques tirages, ces probabilités convergent en moyenne. Pour simuler le modèle, il n’est pas nécessaire (en toute vraisemblance) de parcourir l’univers complet des permutations.
Le tableau 8 indique les intervalles de confiance à 90% que l’on peut construire à partir des simulations précédentes. On obtient une stabilité satisfaisante, bien que les flux agrégés soient stochastiques. Pour une centaine de tirages on peut obtenir une précision supérieure à 10^{-3}.
| e1 | e2 | e3 | |
|---|---|---|---|
| h1 | 2481 |
335 |
334 |
| h2 | 334 |
290 |
51 |
| h3 | 334 |
50 |
290 |
| Source: MEAPS, intervalle à 95%, 1024 tirages | |||
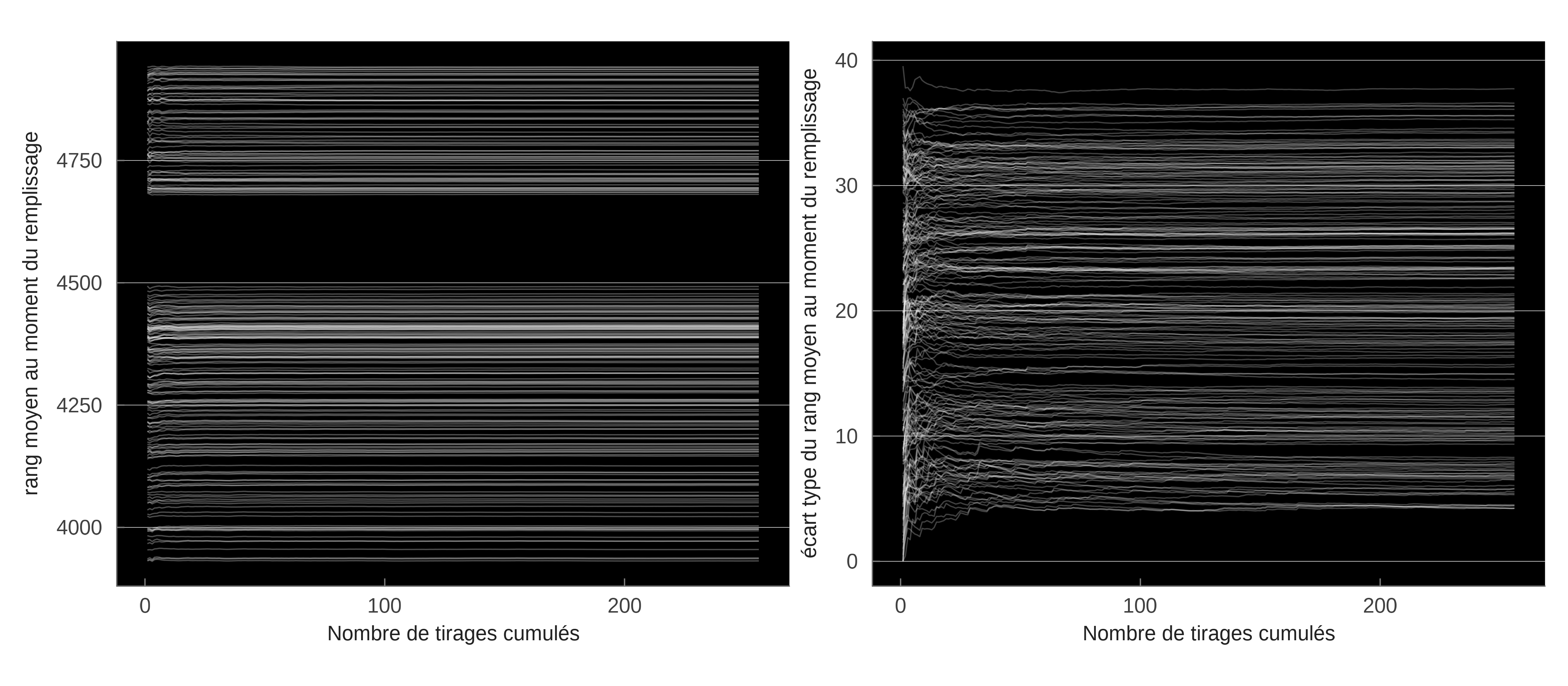
Le schéma de saturation et de priorité est illustré par la figure 6 ci-dessous. Pour chaque carreau d’arrivée (un emploi), on représente le rang moyen (gauche) et son écart-type (droite) au moment de la saturation. La caractère stochastique découle du tirage aléatoire de l’ordre de chaque individu (les carreaux de départ). Pour la plupart des emplois, le rang moyen de saturation ergodique est atteint très rapidement. Les lignes blanches sont rapidement horizontales, indiquant une rapide convergence du rang moyen au fur et à mesure que les tirages s’accumulent. Ce graphique confirme qu’à quelques exceptions près, l’état du système est stable après quelques tirages. Le panneau de droite illustre l’écart-type observé sur les tirages cumulés. La nature stochastique du modèle induite par les tirages est ainsi illustrée.
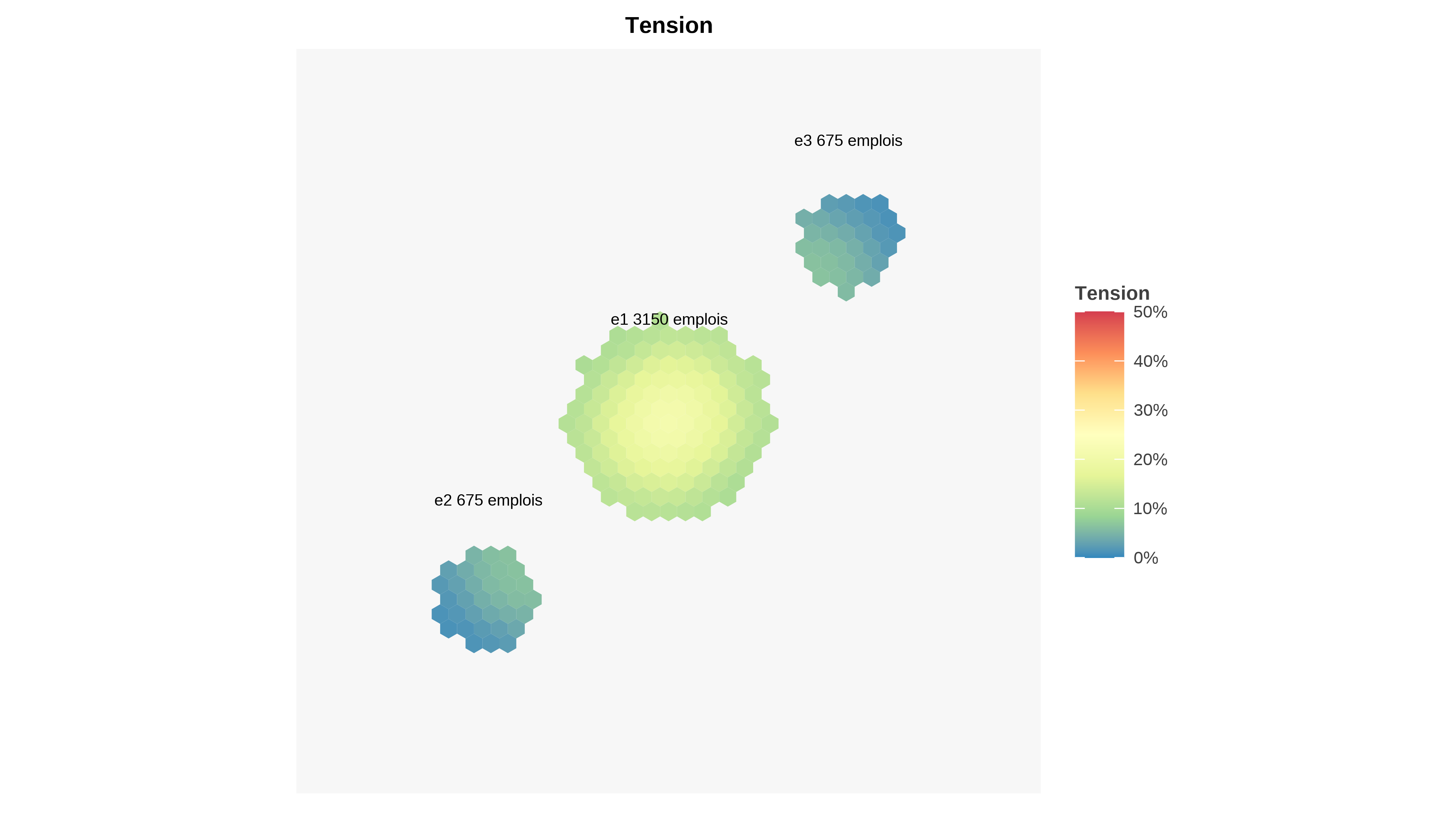
4.5 Tension localisée par emploi
Le rang moyen au moment de la saturation est une information qui peut être utilisé pour construire un indicateur localisé de tension comme sur la figure 7. L’indicateur de tension donne une information distincte de la distance moyenne ou de la densité de population ou d’emploi. Les emplois les plus tendus se trouvent sur l’axe qui relie des pôles. Les emplois situés à la périphérie du pôle central ont un niveau de tension proche (mais un peu supérieur) à ceux situés dans les satellites sur la bordure pointant vers le pôle central. Ces éléments peuvent être utilisés pour identifier les zones pertinentes de développement de l’emploi.
L’expérimentation dans l’application Shiny permet d’étudier différentes propriétés de l’indicateur de tension, en particulier lorsque la tension globale est forte (moins d’emploi que de résidents) ou faible (excès d’emplois sur les résidents). Dans le cas où il y a un excès d’emploi sur les résidents, il est possible d’observer une tension locale sur certains emplois.
4.6 Simulation synthétiques dans Shiny
L’application shiny rmeaps permet de générer des géographies synthétiques et de simuler le modèle MEAPS sur ces distributions. La plupart des graphiques de ce chapitre peuvent être reproduits de cette façon. L’application permet de choisir la taille du problème (n le nombre d’actifs et k le nombre d’emploi). En choisissant plus d’emplois que d’actifs on spécifie un problème où il y a excès d’emplois et donc pas de contrainte globale. Dans le cas inverse, il y a une fuite, calculée de façon à ce que le nombre d’actifs restant sur la zone soit égal au nombre d’emplois.
Différents paramètres permettent de spécifier la géographie, c’est-à-dire la position relative des pôles ou leur taille. Le simulateur simule par Monte-Carlo plusieurs ordres de passages et affiche les graphiques correspondants au fur et à mesure de la convergence, en accumulant la moyenne des différentes variables du modèle. Cette fonctionnalité permet de visualiser simplement la propriété d’ergodicité évoquée plus haut.
Références bibliographiques
Ben-Akiva M., Lerman S.R. (2018). Discrete choice analysis: theory and application to travel demand, MIT Press (Transportation Series).
Commenges H. (2016). « Modèle de radiation et modèle gravitaire - Du formalisme à l’usage », Revue Internationale de Géomatique, 26, n° 1, p. 79‑95.
Dios Ortúzar J. de, Willumsen L.G. (2011). Modelling transport, John wiley & sons.
Fik T.J., Mulligan G.F. (1990). « Spatial Flows and Competing Central Places: Towards a General Theory of Hierarchical Interaction », Environment and Planning A: Economy and Space, 22, n° 4, p. 527‑549.
Floch J.-M., Sillard P. (2019). « Les interactions spatiales. Quelques conséquences de l’introduction du modèle radiatif », Colloque Théo Quant 2019.
Fotheringham A.S. (1983). « A New Set of Spatial-Interaction Models: The Theory of Competing Destinations », Environment and Planning A: Economy and Space, 15, n° 1, p. 15‑36.
Fotheringham A.S. (1984). « Spatial Flows and Spatial Patterns », Environment and Planning A: Economy and Space, 16, n° 4, p. 529‑543.
Hansen W.G. (1959). « How Accessibility Shapes Land Use », Journal of the American Institute of Planners, 25, n° 2, p. 73‑76.
Heanue K.E., Pyers C.E. (1966). « A Comparative Evaluation of Trip Distribution Procedures », Highway Reserach Record, n° 114, p. 20‑50.
INSEE (2022). « Mobilités professionnelles en 2019 : déplacements domicile - lieu de travail Recensement de la population - Base flux de mobilité »,.
Koenig G. (1974). « Theorie economique de l’accessibilite urbaine », Revue économique, 25, n° 2, p. 275.
Koenig G. (1980). « Indicators of urban accessibility: Theory and application », Transportation, 9, n° 2, p. 145‑172.
Lasser J. (2020). « Creating an executable paper is a journey through Open Science », Communications Physics, 3, n° 1.
Lenormand M., Bassolas A., Ramasco J.J. (2016). « Systematic comparison of trip distribution laws and models », Journal of Transport Geography, 51, p. 158‑169.
Masucci A.P., Serras J., Johansson A., Batty M. (2013). « Gravity versus radiation models: On the importance of scale and heterogeneity in commuting flows », Physical Review E, 88, n° 2, p. 022812.
McFadden D. (1974). « The measurement of urban travel demand », Journal of Public Economics, 3, n° 4, p. 303‑328.
Parodi M., Timbeau X. (2024a). « La ville compacte : une solution aux émissions de gaz à effet de serre », Document de travail de l’OFCE, n° 5-2024.
Parodi M., Timbeau X. (2024b). « MEAPS&Gravitaire : Estimations à la Rochelle », Document de travail de l’OFCE, n° 4-2024.
Patrick Bonnel (2001). Prévision de la demande de transport, thèse de doctorat, Lyon, France.
Pirie G.H. (1979). « Measuring Accessibility: A Review and Proposal », Environment and Planning A: Economy and Space, 11, n° 3, p. 299‑312.
Poulit J. (2005). Le Territoire Des Hommes, Éditions Les Pérégrines.
Ruiter E.R. (1967). « Toward a better understanding of the intervening opportunities model », Transportation Research, 1, n° 1, p. 47‑56.
Sen A., Smith T.E. (1995). Gravity Models of Spatial Interaction Behavior, Springer, Berlin, Heidelberg (Advances in Spatial et Network Economics).
Simini F., González M.C., Maritan A., Barabási A.-L. (2012). « A universal model for mobility and migration patterns », Nature, 484, n° 7392, p. 96‑100.
Simini F., Maritan A., Néda Z. (2013). « Human Mobility in a Continuum Approach », PLOS ONE, 8, n° 3, p. e60069.
Stouffer S.A. (1940). « Intervening Opportunities: A Theory Relating Mobility and Distance », American Sociological Review, 5, n° 6, p. 845.
Wilson A.G. (1967). « A statistical theory of spatial distribution models », Transportation Research, 1, n° 3, p. 253‑269.
Réutilisation
Citation
BibTeX
@article{parodi2023,
author = {Parodi, Maxime and Timbeau, Xavier},
title = {MEAPS : Modéliser les flux des navetteurs},
journal = {Document de travail de l’OFCE n°2023-15},
date = {2023-05-02},
url = {https://preview.meaps.fr},
langid = {fr},
abstract = {Le modèle gravitaire utilisé pour distribuer les trajets
entre une origine et une destination représente mal l’influence de
la distance sur les choix. En s’inspirant du modèle des “intervening
opportunities” de @stouffer1940 et du modèle radiatif de
@simini2012, nous construisons un modèle ergodique d’absorption avec
priorité et saturation (MEAPS) qui permet de construire ces choix
sur des fondements microscopiques clairs et flexibles. Le modèle
s’accommode de différentes formulations des processus stochastiques
qui permettent d’estimer des paramètres fondamentaux et de leur
donner une interprétation. Nous validons le modèle théorique sur des
données synthétiques, puis dans deux documents associés
{[}@meaps2024a; @meaps2024b{]}, nous proposons une estimation de
MEAPS et une comparaison détaillée avec le modèle gravitaire et ses
variantes les plus communes. Nous utilisons ensuite cette
modélisation pour construire une carte en haute résolution des
émissions de CO\textasciitilde2\textasciitilde{} à La Rochelle.
\textless br\textgreater{} `r
wordcountaddin::word\_count(“theorie.qmd”)` mots.}
}
Veuillez citer ce travail comme suit :
Parodi M., Timbeau X. (2023). « MEAPS : Modéliser les flux des
navetteurs », Document de travail de l’OFCE
n°2023-15.