MEAPS : Modèle Ergodique d’Absorption avec Priorité et Saturation

Le modèle gravitaire utilisé pour distribuer les trajets entre une origine et une destination représente mal l’influence de la distance sur les choix. En partant du modèle des « intervening opportunities » de Stouffer (1940) et du modèle radiatif de Simini et al. (2012), nous construisons un Modèle Ergodique d’Absorption avec Priorité et Saturation qui permet de construire ces choix sur des fondements microscopiques explicites et flexibles – qui peuvent s’adapter à une grande palette de situations. Ainsi, ce modèle s’accommode de différentes formulations des processus stochastiques microscopiques qui permettent d’estimer des paramètres fondamentaux et de leur donner une interprétation.

Autour de ce modèle nous avons produit trois documents de travail de l’OFCE :

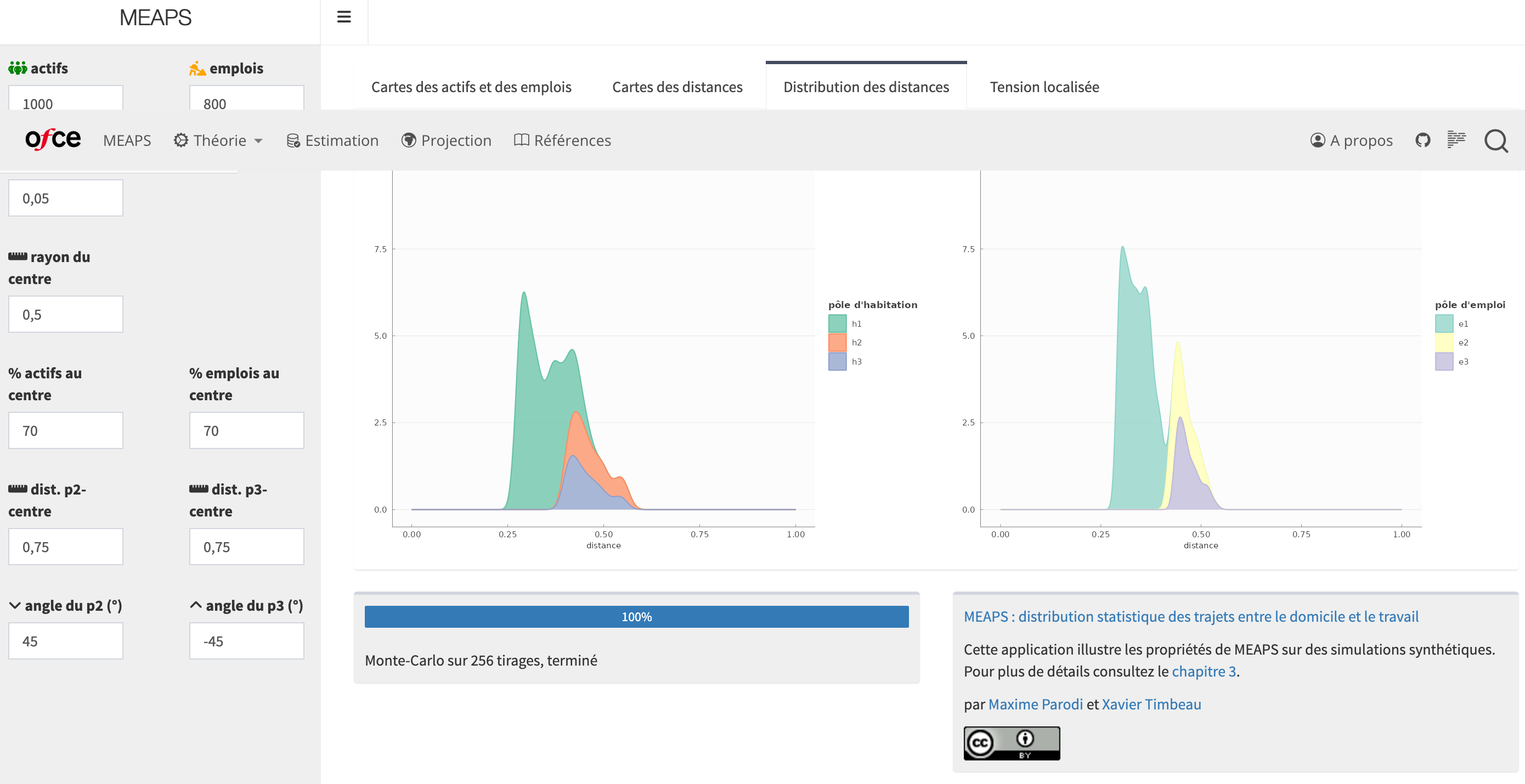
1. Dans le premier document de travail, nous développons les aspects théoriques (Parodi et Timbeau, 2023), nous définissons le modèle et nous en dérivons quelques propriétés théoriques. La logique est de classer pour chaque résident les opportunités qu’il peut atteindre. Ce classement peut être par exemple dans l’ordre défini par les distances. Chaque individu parcoure alors les opportunités et a à chaque rencontre une probabilité de s’arrêter (Absorption). Chaque absorption diminue la quantité d’opportunités disponibles aux autres individus jusqu’à la Saturation. L’affectation des opportunités est faite en fonction d’un ordre de Priorité des individus et nous considérons la moyenne des affectations sur un ensemble d’ordre tirés au sort (Ergodique). A partir de simulations sur des données synthétiques (c’est-à-dire générées par des processus connus dont on définit les paramètres), nous explorons les propriétés du modèle théorique.

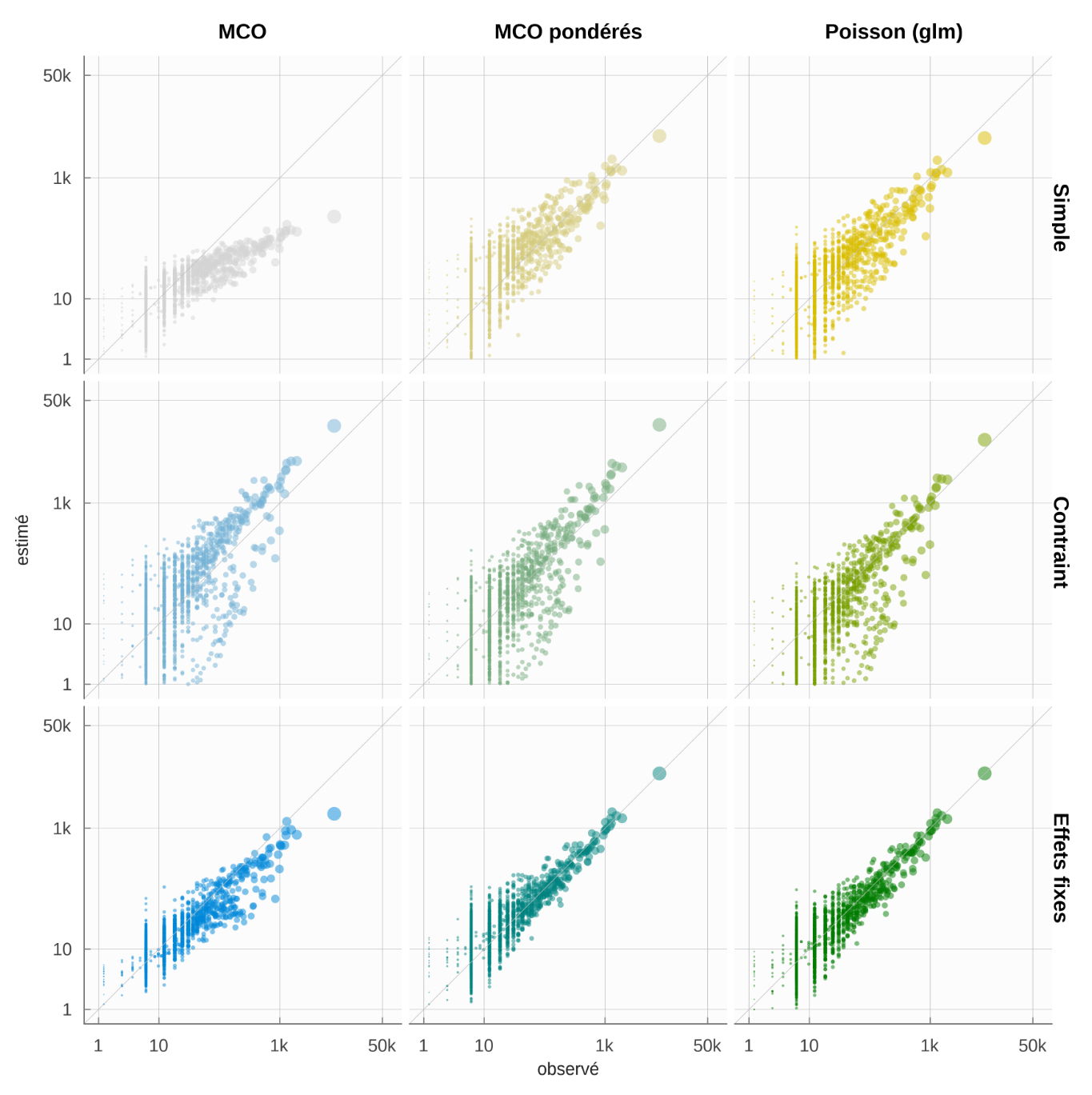
2. Dans le second document de travail, nous ajustons MEAPS sur des données en le comparant aux modèles gravitaires (Parodi et Timbeau, 2024b). Un point important est l’hypothèse faite sur le processus générateur. La nature des données de flux et leur distribution fait privilégier une distribution de Poisson à la distribution log-normale habituellement choisie. Ceci conduit à privilégier la minimisation de l’entropie relative de Kullback-Leibler à la somme des erreurs au carré. En changeant de métrique on peut estimer des modèles par des procédures non linéaires. Nous comparons systématiquement les modèles gravitaires avec MEAPS augmenté de structures particulières sur les odds-ratios et, à moins de le normer localement et globalement, le modèle gravitaire ressort moins pertinent que MEAPS. En effet, deux propriétés importantes doivent être respectées : la séparabilité locale et l’agrégation. Lorsque ces propriétés sont respectées, les modèles ont de bonnes performances hors échantillon. En utilisant une information infracommunale, il est possible d’augmenter la capacité prédictive des modèles, en particulier de MEAPS. Ceci permet également de projeter à une échelle infra-communale les flux simulés.

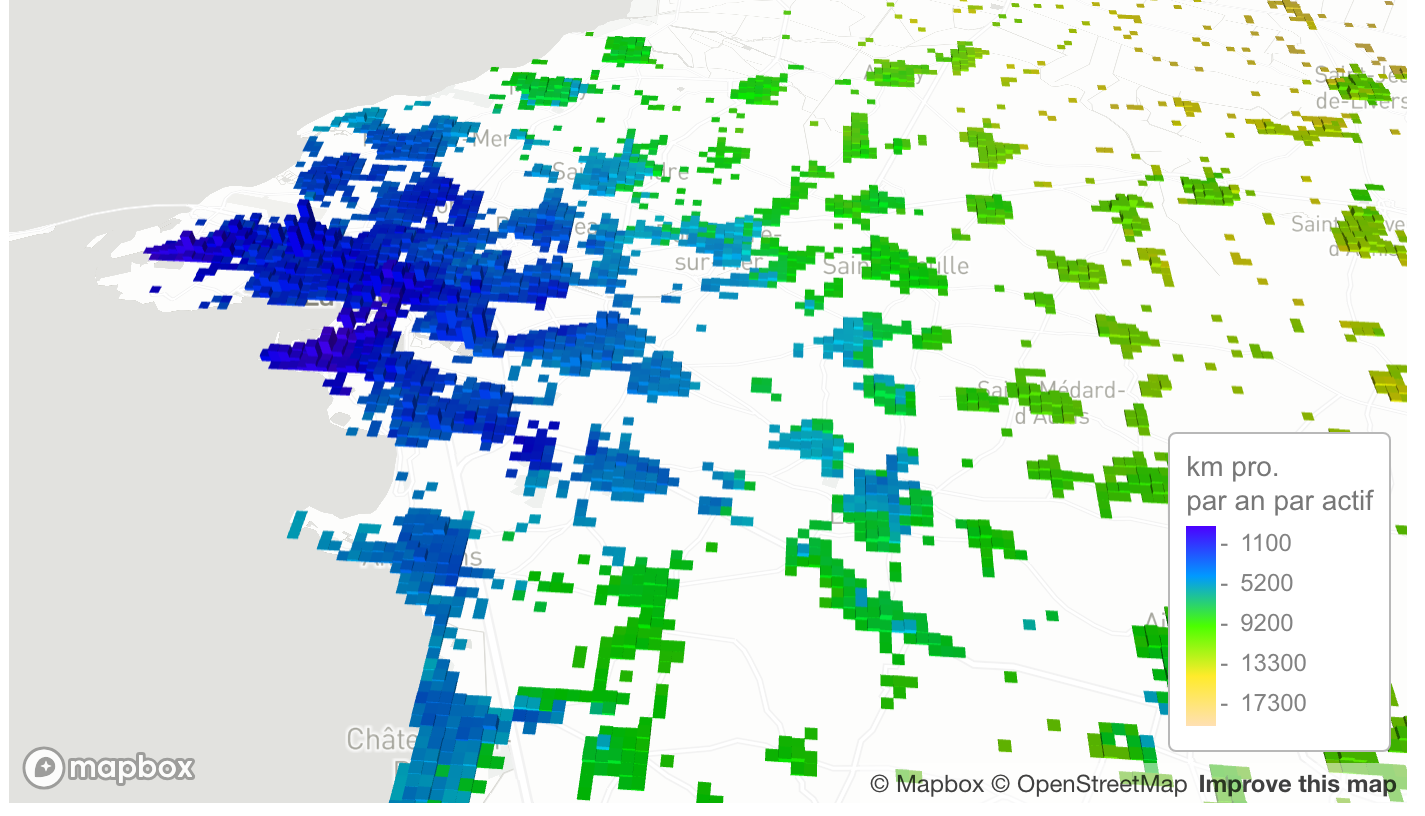
3. Dans un troisième document de travail, nous proposons une application de MEAPS à la Rochelle de la modélisation des trajets quotidiens entre le domicile et le travail (Parodi et Timbeau, 2024a). En ajoutant une modélisation des fréquences de trajets, de leur complexité (multi motifs), des modes de transport, déclinée pour différentes catégories de ménages, nous produisons une cartographie des émissions de CO₂ au carreau 200m. Cette modélisation permet de reprendre la discussion entre densité et émissions de CO₂, que nous retraçons dans la littérature pour conclure que ce lien est plus complexe qu’habituellement considéré. Il est en effet illusoire vouloir capturer la notion de « ville compacte » avec seulement une mesure de la densité ou d’autres métriques (les fameux 3Ds). Il est nécessaire de prendre en compte le lien entre la distribution spatiale des résidents et de leurs centre d’intérêts (ici leurs emplois) pour appréhender l’impact de la forme urbaine et donc disposer d’une modélisation plus riche.

Licence

Cette œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution 4.0 International.

Remerciements

Nous remercions Francesco Pirri et Pablo Vallier pour leur travail durant un stage à l’OFCE pendant l’été 2022 et une trop courte période d’assistant de recherche. Tanguy Enez et Jeanne Devineau ont pris le relais de Pablo et Francesco et ont significativement contribué à leur tour. Les discussions et les travaux conduits (Lempérière et al., 2023) avec Paul Lempérière, David Miet, Lucas Pouvreau et Valentin Stuhlfauth de Villes Vivantes ont été particulièrement fructueux pour l’application à la Rochelle, en partie financée par l’agglomération de la Rochelle. Nous remercions également Florence Nassiet et Bernard Habbouche ainsi que leurs collègues des services de l’agglomération de la Rochelle dont les encouragements et les questionnements nous aurons guidé dans ce travail. L’ensemble des calculs a été réalisé sur nuvolos.cloud dont le support technique s’est avéré indispensable. Tout le reste, et en particulier les erreurs, sont de notre fait.

Code, Shiny, Quarto

Le code utile, principalement en C++, pour les calculs est regroupé dans un package R{rmeaps} accessible dans un dépôt public github.com/maxime2506/rmeaps.

Une application shiny permet de reproduire les simulations synthétiques, accessible à ofce.shinyapps.io/rmeaps dont le code se trouve dans le dépôt github github.com/xtimbeau/meaps.

Ces documents ont été produits avec Quarto. Le document « Aspects théoriques » ne demande rien de plus pour être exécutée qu’un environnement supportant Quarto. La partie Simulations synthétiques est exécutable complètement à partir des fichiers présent dans le dossier R du dépôt github github.com/xtimbeau/meaps. Le document « Estimation à la Rochelle » est exécutable en partie, la partie infracommunale nécessitant l’accès à des données spécifiques pour lesquelles nous étudions la possibilité de diffusion. N’hésitez pas à contacter les auteurs sur ce point.

Nous utilisons de nombreux packages et logiciels libres dont tidyverse, data.table, matrixStats, R5, r5r, Rcpp, OpenMP, quarto, shiny, shinyWidgets, shinydashboard, future, furrr et bien sûr R et RStudio de Posit.

Contacts : Maxime Parodi ou Xavier Timbeau

Lempérière P., Miet D., Parodi M., Pouvreau L., Stulhfauth V., Timbeau X. (2023). « SCoT La Rochelle Aunis : les émissions moyennes des habitants du territoire pour leurs mobilités quotidiennes »,.

Parodi M., Timbeau X. (2023). « MEAPS : modéliser les flux de navetteurs », Document de travail de l’OFCE, n° 15-2023.

Parodi M., Timbeau X. (2024a). « La ville compacte : une solution aux émissions de gaz à effet de serre », Document de travail de l’OFCE, n° 5-2024.

Parodi M., Timbeau X. (2024b). « MEAPS&Gravitaire : Estimations à la Rochelle », Document de travail de l’OFCE, n° 4-2024.

Simini F., González M.C., Maritan A., Barabási A.-L. (2012). « A universal model for mobility and migration patterns », Nature, 484, n° 7392, p. 96‑100.

Stouffer S.A. (1940). « Intervening Opportunities: A Theory Relating Mobility and Distance », American Sociological Review, 5, n° 6, p. 845.